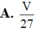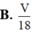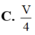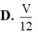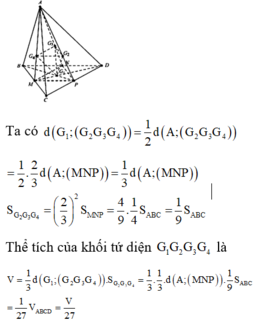Các câu hỏi tương tự
Cho tứ diện ABCD có thể tích bằng 12 và G là trọng tâm của tam giác BCD. Tính thể tích V của khối chóp A.GBC
A. V=3
B. V=4
C. V=5
D. V=6
Cho tứ diện ABCD có đáy BCD là tam giác đều, trọng tâm G.
∆
là đường thẳng qua G và vuông góc với (BCD). A chạy trên
∆
sao cho mặt câu ngoại tiếp ABCD có thể tích nhỏ nhất. Khi đó thể tích khối ABCD là:
A
.
a
3
12
B
.
a
3
2...
Đọc tiếp
Cho tứ diện ABCD có đáy BCD là tam giác đều, trọng tâm G. ∆ là đường thẳng qua G và vuông góc với (BCD). A chạy trên ∆ sao cho mặt câu ngoại tiếp ABCD có thể tích nhỏ nhất. Khi đó thể tích khối ABCD là:
A . a 3 12
B . a 3 2 12
C . a 3 3 12
D . a 3 3 6
Cho khối tứ diện ABCD có thể tích V. Gọi
G
1
G
2
G
3
G
4
là trọng tâm của 4 mặt của tứ diện ABCD. Thể tích của khối tứ diện
G
1
G
2
G
3
G
4
là A....
Đọc tiếp
Cho khối tứ diện ABCD có thể tích V. Gọi G 1 G 2 G 3 G 4 là trọng tâm của 4 mặt của tứ diện ABCD. Thể tích của khối tứ diện G 1 G 2 G 3 G 4 là
A. V 27
B. V 18
C. V 4
D. V 12
Cho tứ diện đều ABCD có cạnh a. Gọi G, G’ lần lượt là trọng tâm của tam giác ABC và ABD. Diện tích của thiết diện của hình tứ diện khi cắt bởi mặt phẳng (BGG’) là: A. B. C. D.
Đọc tiếp
Cho tứ diện đều ABCD có cạnh a. Gọi G, G’ lần lượt là trọng tâm của tam giác ABC và ABD. Diện tích của thiết diện của hình tứ diện khi cắt bởi mặt phẳng (BGG’) là:
A. ![]()
B. ![]()
C. ![]()
D. 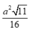
Cho tứ diện ABCD cạnh a. Gọi G là trọng tâm của tam giác ABC. Qua G dựng một mặt phẳng (P) song song với mặt phẳng (P) song song với mặt phẳng (BCD). Tìm diện tích thiết diện của (P) và tứ diện ABCD. A.
a
2
3
4
B.
a
2
3
9
C. ...
Đọc tiếp
Cho tứ diện ABCD cạnh a. Gọi G là trọng tâm của tam giác ABC. Qua G dựng một mặt phẳng (P) song song với mặt phẳng (P) song song với mặt phẳng (BCD). Tìm diện tích thiết diện của (P) và tứ diện ABCD.
A. a 2 3 4
B. a 2 3 9
C. a 2 2 16
D. a 2 3 18
Cho tứ diện đều ABCD có cạnh bằng a. Gọi G là trọng tâm tam giác ABC. Mặt phẳng (GCD) cắt tứ diện theo 1 thiết diện có diện tích là A.
a
2
3
2
.
B.
a
2
2
4
.
C.
a
2...
Đọc tiếp
Cho tứ diện đều ABCD có cạnh bằng a. Gọi G là trọng tâm tam giác ABC. Mặt phẳng (GCD) cắt tứ diện theo 1 thiết diện có diện tích là
A. a 2 3 2 .
B. a 2 2 4 .
C. a 2 2 6 .
D. a 2 4 4 .
Cho hình tứ diện đều ABCD có cạnh bằng 3. Gọi
G
1
,
G
2
,
G
3
,
G
4
là trọng tâm của bốn mặt của tứ diện ABCD. Tính thể tích V của khối tứ diện
G
1
G
2
G
3...
Đọc tiếp
Cho hình tứ diện đều ABCD có cạnh bằng 3. Gọi G 1 , G 2 , G 3 , G 4 là trọng tâm của bốn mặt của tứ diện ABCD. Tính thể tích V của khối tứ diện G 1 G 2 G 3 G 4 .
A. V = 2 4
B. V = 2 18
C. V = 2 32
D. V = 2 12
Cho tứ diện ABCD. Gọi G là trọng tâm của ΔBCD. Hai điểm M và N lần lượt thuộc cạnh BC,CD sao cho \(\dfrac{BM}{BC}=\dfrac{1}{4};\dfrac{NC}{ND}=\dfrac{3}{2}\). Chứng minh A,M,N,G đồng phẳng
Cho tứ diện ABCD. gọi G₁, G₂ là trọng tâm ∆ABD và ∆ACD. C/m: G₁ G₂ // (ABC) G₁ G₂ // (BCD)