1B

2A

3A

4C

đề bài đầy đủ: rút gọn các biểu thức lượng giác sau trên điều kiện xác định của chúng:

\(\frac{sin^2x}{cosx+cosx.\frac{sinx}{cosx}}-\frac{cos^2x}{sinx+sinx.\frac{cosx}{sinx}}=\frac{sin^2x}{sinx+cosx}-\frac{cos^2x}{sinx+cosx}=\frac{sin^2x-cos^2x}{sinx+cosx}\)

\(=\frac{\left(sinx+cosx\right)\left(sinx-cosx\right)}{sinx+cosx}=sinx-cosx\)

\(\left(\frac{sinx}{cosx}+\frac{cosx}{1+sinx}\right)\left(\frac{cosx}{sinx}+\frac{sinx}{1+cosx}\right)=\left(\frac{sinx+sin^2x+cos^2x}{cosx\left(1+sinx\right)}\right)\left(\frac{cosx+cos^2x+sin^2x}{sinx\left(1+cosx\right)}\right)\)

\(=\left(\frac{sinx+1}{cosx\left(1+sinx\right)}\right)\left(\frac{cosx+1}{sinx\left(1+cosx\right)}\right)=\frac{1}{sinx.cosx}\)

a/ \(cosx>0\Rightarrow cosx=\sqrt{1-sin^2x}=\frac{4}{5}\)

\(\Rightarrow tanx=-\frac{3}{4}\Rightarrow A=\frac{129}{20}\)

b/ \(B=\frac{5sinx+3cosx}{3cosx-2sinx}=\frac{\frac{5sinx}{sinx}+\frac{3cosx}{sinx}}{\frac{3cosx}{sinx}-\frac{2sinx}{sinx}}=\frac{5+3cotx}{3cotx-2}=\frac{5+9}{9-2}\)

c/ \(C=\frac{sinx.cosx\left(cotx-2tanx\right)}{sinx.cosx\left(5cotx+tanx\right)}=\frac{cos^2x-2sin^2x}{5cos^2x+sin^2x}=\frac{cos^2x-2\left(1-cos^2x\right)}{5cos^2x+1-cos^2x}=\frac{3cos^2x-2}{4cos^2x+1}=...\)

d/ Không dịch được đề, ko biết mẫu số bên trái nó đến đâu cả

1.

ĐK: \(x\ne\dfrac{k\pi}{2}\)

\(cotx-tanx=sinx+cosx\)

\(\Leftrightarrow\dfrac{cosx}{sinx}-\dfrac{sinx}{cosx}=sinx+cosx\)

\(\Leftrightarrow\dfrac{cos^2x-sin^2x}{sinx.cosx}=sinx+cosx\)

\(\Leftrightarrow\left(\dfrac{cosx-sinx}{sinx.cosx}-1\right)\left(sinx+cosx\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}sinx+cosx=0\left(1\right)\\cosx-sinx=sinx.cosx\left(2\right)\end{matrix}\right.\)

\(\left(1\right)\Leftrightarrow\sqrt{2}sin\left(x+\dfrac{\pi}{4}\right)=0\Leftrightarrow x=-\dfrac{\pi}{4}+k\pi\)

\(\left(2\right)\Leftrightarrow t=\dfrac{1-t^2}{2}\left(t=cosx-sinx,\left|t\right|\le2\right)\)

\(\Leftrightarrow t^2+2t-1=0\)

\(\Leftrightarrow\left[{}\begin{matrix}t=-1+\sqrt{2}\\t=-1-\sqrt{2}\left(l\right)\end{matrix}\right.\)

\(\Leftrightarrow cosx-sinx=-1+\sqrt{2}\)

\(\Leftrightarrow-\sqrt{2}sin\left(x-\dfrac{\pi}{4}\right)=-1+\sqrt{2}\)

\(\Leftrightarrow sin\left(x-\dfrac{\pi}{4}\right)=\dfrac{\sqrt{2}-1}{\sqrt{2}}\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{4}+arcsin\left(\dfrac{\sqrt{2}-1}{\sqrt{2}}\right)+k2\pi\\x=\dfrac{5\pi}{4}-arcsin\left(\dfrac{\sqrt{2}-1}{\sqrt{2}}\right)+k2\pi\end{matrix}\right.\)

Vậy phương trình đã cho có nghiệm:

\(x=-\dfrac{\pi}{4}+k\pi;x=\dfrac{\pi}{4}+arcsin\left(\dfrac{\sqrt{2}-1}{\sqrt{2}}\right)+k2\pi;x=\dfrac{5\pi}{4}-arcsin\left(\dfrac{\sqrt{2}-1}{\sqrt{2}}\right)+k2\pi\)

1.

Đặt \(sinx+cosx=t\Rightarrow\left\{{}\begin{matrix}\left|t\right|\le\sqrt{2}\\sinx.cosx=\frac{t^2-1}{2}\end{matrix}\right.\)

Pt trở thành:

\(t^3+\frac{t^2-1}{2}-1=0\)

\(\Leftrightarrow2t^3+t^2-3=0\)

\(\Leftrightarrow\left(t-1\right)\left(2t^2+3t+3\right)=0\)

\(\Leftrightarrow t=1\)

\(\Leftrightarrow sin\left(x+\frac{\pi}{4}\right)=\frac{\sqrt{2}}{2}\)

\(\Leftrightarrow\left[{}\begin{matrix}x+\frac{\pi}{4}=\frac{\pi}{4}+k2\pi\\x+\frac{\pi}{4}=\frac{3\pi}{4}+k2\pi\end{matrix}\right.\)

\(\Leftrightarrow...\)

b.

Đặt \(sinx+cosx=t\Rightarrow\left\{{}\begin{matrix}\left|t\right|\le\sqrt{2}\\sin2x=2sinx.cosx=t^2-1\end{matrix}\right.\)

Pt trở thành:

\(t^4-3\left(t^2-1\right)-1=0\)

\(\Leftrightarrow t^4-3t^2+2=0\)

\(\Leftrightarrow\left[{}\begin{matrix}t^2=1\\t^2=2\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}1+sin2x=1\\1+sin2x=2\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}sin2x=0\\sin2x=1\end{matrix}\right.\)

\(\Leftrightarrow...\)

3.

\(\Leftrightarrow\left(sinx+cosx\right)\left(1-sinx.cosx\right)+2\left(sinx+cosx\right)-6sinx.cosx=0\)

Đặt \(sinx+cosx=t\Rightarrow\left\{{}\begin{matrix}\left|t\right|\le\sqrt{2}\\sinx.cosx=\frac{t^2-1}{2}\end{matrix}\right.\)

Pt trở thành:

\(t\left(1-\frac{t^2-1}{2}\right)+2t-3\left(t^2-1\right)=0\)

\(\Leftrightarrow-t^3-6t^2+7t+6=0\)

Nghiệm của pt bậc 3 này rất xấu, chắc bạn ghi ko đúng đề bài

Chọn C

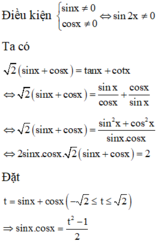
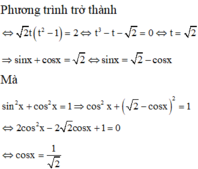
Bổ trợ kiến thức: Ta có thế giải bằng máy tính cầm tay CASIO fx-570VN PLUS như sau, đầu tiên dùng lệnh SHIFT SOLVE để xem 1 nghiệm bất kì có thể có của phương trình đã cho:

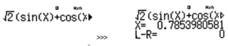
Tiếp theo ta tính cos x thì dễ thấy được:

Đến đây ta dễ dàng chọn được phương án C là phương án đúng thay cho lời giải tự luận nhiều phức tạp.

\(\dfrac{tanx}{sinx}-\dfrac{sinx}{cotx}=cosx\)

\(\Leftrightarrow\dfrac{\dfrac{sinx}{cosx}}{sinx}-\dfrac{sinx}{\dfrac{cosx}{sinx}}=cosx\)

\(\Leftrightarrow\dfrac{1}{cosx}-\dfrac{sin^2x}{cosx}=cosx\)

\(\Leftrightarrow\dfrac{cos^2x}{cosx}=cosx\)

\(\Rightarrowđpcm\)

xin lỗi mik mới lớp 8 thui  kg jup dc j ròi

giup minh giai toan voi

toán nào vậy bạn Hưng

ĐKXĐ:

29.

\(\left\{{}\begin{matrix}cosx\ne0\\sinx\ne0\end{matrix}\right.\) \(\Leftrightarrow sinx.cosx\ne0\)

\(\Leftrightarrow sin2x\ne0\Leftrightarrow x\ne\frac{k\pi}{2}\)

30.

\(\left\{{}\begin{matrix}sinx\ne0\\cosx\ne0\end{matrix}\right.\) \(\Leftrightarrow x\ne\frac{k\pi}{2}\) (như câu trên)

31.

\(sinx\ne0\Leftrightarrow x\ne k\pi\)

32.

\(\left\{{}\begin{matrix}sinx\ne0\\cosx\ne0\\sin2x\ne1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}sin2x\ne0\\sin2x\ne1\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x\ne\frac{k\pi}{2}\\x\ne\frac{\pi}{2}+k2\pi\end{matrix}\right.\)

33.

\(\left\{{}\begin{matrix}cosx\ne0\\cos\frac{x}{2}\ne0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x\ne\frac{\pi}{2}+k\pi\\x\ne\pi+k2\pi\end{matrix}\right.\)

34.

\(\left\{{}\begin{matrix}sinx\ne0\\cosx\ne0\\cotx\ne1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}sin2x\ne0\\cotx\ne1\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x\ne\frac{k\pi}{2}\\x\ne\frac{\pi}{4}+k\pi\end{matrix}\right.\)

35.

\(\left\{{}\begin{matrix}sinx\ne0\\cosx\ne1\end{matrix}\right.\) \(\Leftrightarrow sinx\ne0\)

\(\Leftrightarrow x\ne k\pi\)

36.

\(sin^2x-cos^2x\ne0\Leftrightarrow cos2x\ne0\)

\(\Leftrightarrow x\ne\frac{\pi}{4}+\frac{k\pi}{2}\)

37.

\(cos3x\ne cosx\Leftrightarrow\left\{{}\begin{matrix}3x\ne x+k2\pi\\3x\ne-x+k2\pi\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x\ne k\pi\\x\ne\frac{k\pi}{2}\end{matrix}\right.\) \(\Leftrightarrow x\ne\frac{k\pi}{2}\)

38.

\(\left\{{}\begin{matrix}x\ge0\\sin\pi x\ne0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\\pi x\ne k\pi\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\x\ne k\end{matrix}\right.\)

39.

\(\left\{{}\begin{matrix}cos\left(x-\frac{\pi}{3}\right)\ne0\\tan\left(x-\frac{\pi}{3}\right)\ne-1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x-\frac{\pi}{3}\ne\frac{\pi}{2}+k\pi\\x-\frac{\pi}{3}\ne-\frac{\pi}{4}+k\pi\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x\ne\frac{5\pi}{6}+k\pi\\x\ne-\frac{\pi}{12}+k\pi\end{matrix}\right.\)