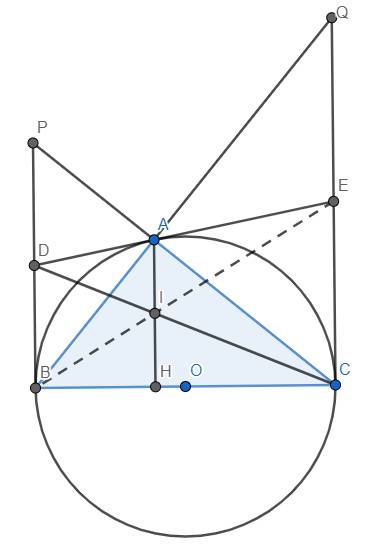
cho tam giác ABC vuông tại A, đường cao AH . O là tâm đường tròn ngoại tiếp tam giác ABC , d là tiếp tuyến của đường tròn tâm O tại A. Các tiếp tuyến của đường tròn tại B và C cắt d theo thứ tự tại D và E .Gọi M là giao điểm của OD và AB , N là giao điểm của EO và AC
a) Tính số đo góc DOE. chứng minh AMON là hình chữ nhật
b) Chứng minh : DE=BD+CE và BD.CE =R2
c) Cho AB = 6cm, AC =8cm. Tính khoảng cách từ A đến đường kính BC của đường tròn tâm O
d) Chứng minh rằng BC là tiếp tuyến của đường tròn đường kính DE