Vẽ đồ thị hàm số:
a) \(y=\left|x\right|+1\)
\(b\) ) \(y=2x+\left|1-2x\right|\)
Những câu hỏi liên quan
a) khảo sát và vẽ đồ thị hàm số \(y=\dfrac{2x-3}{x+2}\)
b) khảo sát và vẽ đồ thị hàm số \(y=\left|\dfrac{2x-3}{x+2}\right|\)
c) khảo sát và vẽ đồ thị hàm số \(y=\dfrac{2x-3}{\left|x+2\right|}\)
a) khảo sát và vẽ đồ thị hàm số \(y=x^4-2x^2+3\)
b) vẽ đồ thị hàm số \(y=\left|x^4-2x^2+3\right|\)
Vẽ đồ thị các hàm số :
a. \(y=\left\{{}\begin{matrix}2x;\left(x\ge0\right)\\-\dfrac{1}{2}x;\left(x< 0\right)\end{matrix}\right.\)
b. \(y=\left\{{}\begin{matrix}x+1;\left(x\ge1\right)\\-2x+4;\left(x< 1\right)\end{matrix}\right.\)
a. Vẽ đồi thị hàm số y= 2x +3
b. Xác định m để đồ thị hàm số y= 2x +3 song song với đồ thị hàm số \(y=\left(m^2-2m+2\right)x+2m-1\)
Cho hàm số y = -2x
a) Vẽ đồ thị của hàm số
b) Trong các điểm \(M\left(3;6\right),N\left(-2;4\right),P\left(\frac{1}{2};-2\right)\), điểm nào thuộc đồ thị hàm số
Cho hàm số yfleft(xright) có đạo hàm liên tục trên R, thỏa mãn: 2fleft(2xright)+fleft(1-2xright)12x^2. Phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ x1 là:A. y4x-2B. y2x+2C. y2x-6D. y4x-6
Đọc tiếp
Cho hàm số \(y=f\left(x\right)\) có đạo hàm liên tục trên R, thỏa mãn: \(2f\left(2x\right)+f\left(1-2x\right)=12x^2\). Phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ \(x=1\) là:
A. \(y=4x-2\)
B. \(y=2x+2\)
C. \(y=2x-6\)
D. \(y=4x-6\)
SGK Toán 10 tập 2 - Bộ sách Kết nối tri thức với cuộc sống - Trang 9
30 tháng 9 2023 lúc 9:10
Vẽ đồ thị của các hàm số \(y=3x+1\) và \(y=-2x^2\). Hãy cho biết:
a) Hàm số \(y=3x+1\) đồng biến hay nghịch biến trên R.
b) Hàm số \(y=-2x^2\) đồng biến hay nghịch biến trên mỗi khoảng: \(\left(-\infty;0\right)\) và \(\left(0;+\infty\right)\)
Vẽ đồ thị \(y = 3x + 1;y = - 2{x^2}\)
a) Trên \(\mathbb{R}\), đồ thị \(y = 3x + 1\) đi lên từ trái sang phải, như vậy hàm số \(y = 3x + 1\) đồng biến trên \(\mathbb{R}\)
b) Trên khoảng \(\left( { - \infty ;0} \right)\), đồ thị \(y = - 2{x^2}\)đi lên từ trái sang phải với mọi \(x \in \left( { - \infty ;0} \right)\) , như vậy hàm số đồng biến trên \(\left( { - \infty ;0} \right)\)
Trên khoảng \(\left( {0; + \infty } \right)\), đồ thị \(y = - 2{x^2}\)đi xuống từ trái sang phải với mọi \(x \in \left( {0; + \infty } \right)\) , như vậy hàm số nghịch biến trên \(\left( {0; + \infty } \right)\)
Đúng 0
Bình luận (0)
11 tháng 5 2022 lúc 22:10
Cho hàm đa thức yleft[fleft(x^2+2xright)right] có đồ thị cắt trục Ox tại 5 điểm phân biệt như hình vẽ. Hỏi có bao nhiêu giá trị của tham số m2022min Z để hàm số gleft(xright)fleft(x^2-2left|x-1right|-2x+mright) có 9 điểm cực trị?Giúp mình với ạ, mình cảm ơn nhiều♥
Đọc tiếp
Cho hàm đa thức \(y=\left[f\left(x^2+2x\right)\right]'\) có đồ thị cắt trục \(Ox\) tại 5 điểm phân biệt như hình vẽ. Hỏi có bao nhiêu giá trị của tham số \(m=2022m\in Z\) để hàm số \(g\left(x\right)=f\left(x^2-2\left|x-1\right|-2x+m\right)\) có 9 điểm cực trị?
Giúp mình với ạ, mình cảm ơn nhiều♥
đề bài thiếu, ko giải được, cái nghiệm -1 có thể của f(u) hoặc của u'
Đúng 0
Bình luận (1)
6 tháng 9 2023 lúc 21:32
Cho hàm số ymx+3 có đồ thị là left(d_1right) và hàm số ydfrac{-1}{m}x+3left(mne0right) có đồ thị left(d_2right)1) Với m 1 a) Vẽ đồ thị left(d_1right) và left(d_2right) trên cùng một mặt phẳng tọa độ b) Tìm tọa độ giao điểm của left(d_1right) và left(d_2right).
Đọc tiếp
Cho hàm số \(y=mx+3\) có đồ thị là \(\left(d_1\right)\) và hàm số \(y=\dfrac{-1}{m}x+3\left(m\ne0\right)\) có đồ thị \(\left(d_2\right)\)
1) Với m = 1
a) Vẽ đồ thị \(\left(d_1\right)\) và \(\left(d_2\right)\) trên cùng một mặt phẳng tọa độ
b) Tìm tọa độ giao điểm của \(\left(d_1\right)\) và \(\left(d_2\right)\).
1: Khi m=1 thì (d1): y=x+3 và (d2): y=-x+3
a: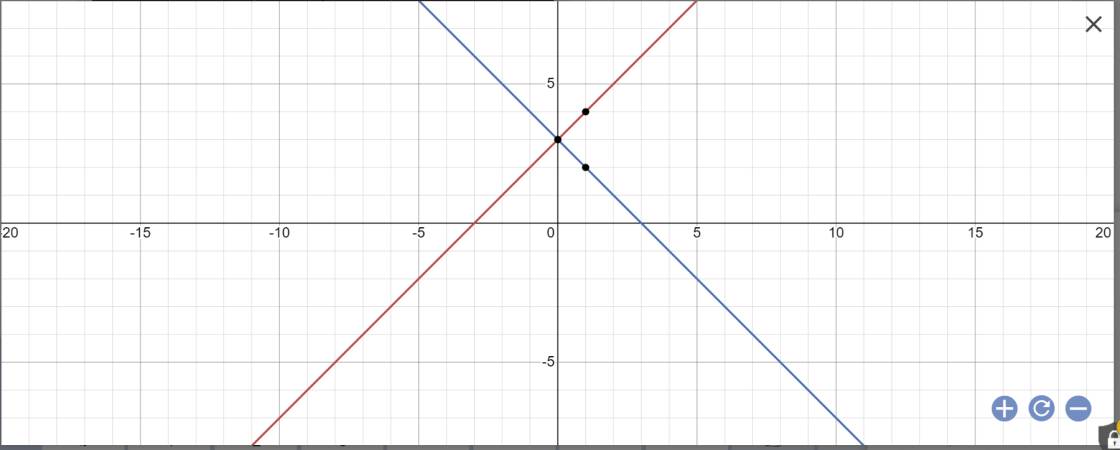 
b: Tọa độ giao điểm là:
x+3=-x+3 và y=x+3
=>x=0 và y=3
Đúng 2
Bình luận (0)