Cho hàm số \(y=\left(3m-2\right)x-6m+5\)
Tìm m để khoảng cách từ gốc O đến đồ thị hàm số lớn nhất
tìm m để đồ thị hàm số \(\left(C_m\right):y=x^3-3mx^2+3\left(m^2-1\right)x-m^3+m\) có cực trị đồng thời khoảng cách từ điểm cực đại của đồ thị hàm số O bằng √2 lần khoảng cách từ điểm cực tiểu của đồ thị hàm số đến O ( O là gốc tọa độ )
Lời giải:
$y'=3x^2-6mx+3(m^2-1)=0$
$\Leftrightarrow x^2-2mx+m^2-1=0$
$\Leftrightarrow x=m+1$ hoặc $x=m-1$
Với $x=m+1$ thì $y=-2m-2$. Ta có điểm cực trị $(m+1, -2m-2)$
Với $x=m-1$ thì $y=2-2m$. Ta có điểm cực trị $m-1, 2-2m$
$f''(m+1)=6>0$ nên $A(m+1, -2m-2)$ là điểm cực tiểu
$f''(m-1)=-6< 0$ nên $B(m-1,2-2m)$ là điểm cực đại
$BO=\sqrt{2}AO$
$\Leftrightarrow BO^2=2AO^2$
$\Leftrightarrow (m-1)^2+(2-2m)^2=2(m+1)^2+2(-2m-2)^2$
$\Leftrightarrow m=-3\pm 2\sqrt{2}$
tìm m để đồ thị hàm số \(\left(C_m\right):y=x^3-3mx^2+3\left(m^2-1\right)x-m^3+m\) có cực trị đồng thời khoảng cách từ điểm cực đại của đồ thị hàm số O bằng \(\sqrt{2}\) lần khoảng cách từ điểm cực tiểu của đồ thị hàm số đến O ( O là gốc tọa độ )
cho hàm số \(y=\left(m-1\right)x+3m\)
tìm m để khoảng cách từ tâm O tới đồ thị hàm số trên đạt max
PT giao Ox: \(y=0\Leftrightarrow\left(m-1\right)x=-3m\Leftrightarrow x=\dfrac{3m}{1-m}\Leftrightarrow A\left(\dfrac{3m}{1-m};0\right)\Leftrightarrow OA=\left|\dfrac{3m}{1-m}\right|\)
PT giao Oy: \(x=0\Leftrightarrow y=3m\Leftrightarrow B\left(0;3m\right)\Leftrightarrow OB=\left|3m\right|\)
Gọi H là hình chiếu O lên đths
K/c từ O đến đths đạt max khi OH đạt max
Áp dụng HTL: \(\dfrac{1}{OH^2}=\dfrac{1}{OA^2}+\dfrac{1}{OB^2}\)
\(\Leftrightarrow\dfrac{1}{OH^2}=\dfrac{\left(1-m\right)^2}{9m^2}+\dfrac{1}{9m^2}=\dfrac{m^2-2m+2}{9m^2}\)
Đặt \(\dfrac{1}{OH^2}=t\Leftrightarrow9m^2t=m^2-2m+2\)
\(\Leftrightarrow m^2\left(9t-1\right)+2m-2=0\)
Coi đây là PT bậc 2 ẩn m, PT có nghiệm khi:
\(\Delta=4-4\left(-2\right)\left(9t-1\right)\ge0\\ \Leftrightarrow4+72t-9\ge0\\ \Leftrightarrow t\ge\dfrac{5}{72}\Leftrightarrow\dfrac{1}{OH^2}\ge\dfrac{5}{72}\\ \Leftrightarrow OH^2\le\dfrac{72}{5}\Leftrightarrow OH\le\dfrac{6\sqrt{10}}{5}\)
Dấu \("="\Leftrightarrow\) PT có nghiệm kép
\(\Leftrightarrow m=-\dfrac{b}{2a}=-\dfrac{2}{18t-2}=-\dfrac{2}{18\cdot\dfrac{5}{72}-2}=\dfrac{8}{3}\)
cho hàm số y=(m+1)x+3. tìm m để khoảng cách từ gốc tọa độ đến đồ thị hàm số có giá trị lớn nhất
Đặt: d: y = ( m+1 ) x + 3
+) TH1: m = -1
=> d: y = 3
=> Khoảng cách của gốc tọa độ tới d là: 3 (1)
+) Th2: m khác -1.
Giao điểm của d với Ox là : A ( \(-\frac{3}{m+1};0\))
=> \(OA=\left|\frac{3}{m+1}\right|\)
Giao điểm của d với Oy là: \(B\left(0;3\right)\)
=> OB = 3.
Kẻ OH vuông với d tại H => AH là khoảng cách từ O tới d
Xét tam giác OAB vuông tại O. Có OH là đường cao:
=> \(\frac{1}{OH^2}=\frac{1}{OA^2}+\frac{1}{OB^2}=\frac{\left(m+1\right)^2}{9}+\frac{1}{9}>\frac{1}{9}\)vì m khác 1 => \(\left(m+1\right)^2>0\)
=> \(OH< 3\)
=> Khoảng cách từ gốc tọa độ đến d nhỏ hơn 3 (2)
Từ (1); (2) Khoảng cách từ O đến d có giá trị lớn nhất là 3 đạt tại m = -1.
len google bn oi
Cho hàm số y = -mx + m+2 có đồ thị là (d). Tìm m để khoảng cách từ gốc tọa độ O đến (d) là lớn nhất
Cho hàm số y = (2m+2)x + m -1. Tìm m để khoảng cách từ O đến đồ thị hàm số trên là lớn nhất.
Nếu \(2m+2=0\Rightarrow m=-1\Rightarrow y=-2\)
=> ĐTHS là đường thẳng đi qua (0;-2) và // với trục Ox
=> Khoảng cách từ O đến đths là 2
Nếu \(2m+2\ne0\Rightarrow m\ne-1\)
Khi đó ĐTHS \(y=\left(2m+2\right)x+m-1\) là đường thẳng đi qua điểm \(A\left(\frac{1-m}{2m+2};0\right)\) và \(B\left(0;m-1\right)\)
(ĐTHS bạn tự vẽ nhé)
Kẻ OH vuông góc với AB => OH là khoảng cách từ O đến đths
Tam giác AOB vuông tại O có OH là đường cao ứng với cạnh huyền nên ta có hệ thức sau:
\(\frac{1}{OH^2}=\frac{1}{OA^2}+\frac{1}{OB^2}=\frac{1}{\left(\frac{1-m}{2m+2}\right)^2}+\frac{1}{\left(m-1\right)^2}=\frac{4m^2+8m+5}{m^2-2m+1}\)
\(\Rightarrow OH^2=\frac{m^2-2m+1}{4m^2+8m+5}\)
Đặt \(OH^2=a\ge0\)
\(\Rightarrow4m^2a+8ma+5a=m^2-2m+1\)
\(\Leftrightarrow m^2\left(4a-1\right)+2m\left(4a+1\right)+\left(5a-1\right)=0\)
\(\Delta^'=\left(4a+1\right)^2-\left(4a-1\right)\left(5a-1\right)=16a^2+8a+1-20a^2+9a-1\)
\(=-4a^2+17a=-a\left(4a-17\right)\)
\(\Delta^'\ge0\Leftrightarrow a\left(4a-17\right)\le0\Rightarrow0\le a\le\frac{17}{4}\)
\(\Rightarrow a_{max}=\frac{17}{4}\Rightarrow OH^2=\frac{17}{4}\Rightarrow OH=\frac{\sqrt{17}}{2}\)
Dấu "=" xảy ra khi: \(\frac{m^2-2m+1}{4m^2+8m+5}=\frac{17}{4}\Leftrightarrow4m^2-8m+4=68m^2+136m+85\)
\(\Leftrightarrow64m^2+144m+81=0\Leftrightarrow\left(8m+9\right)^2=0\Rightarrow m=-\frac{9}{8}\)
Vậy khoảng cách lớn nhất từ O đến đths là \(\frac{\sqrt{17}}{2}\) khi \(m=-\frac{9}{8}\)
Tìm tất cả các giá trị thực của tham số m để hàm số y = x 3 - 3 m x 2 + 3 ( m 2 - 1 ) x - m 3 + m có cực trị đồng thời khoảng cách từ điểm cực đại của đồ thị hàm số đến gốc tọa độ O bằng 2 lần khoảng cách từ điểm cực tiểu của đồ thị hàm số đến gốc tọa độ O
A. m = - 3 - 2 2 h o ặ c m = - 1
B. m = - 3 + 2 2 h o ặ c m = - 1
C. m = - 3 + 2 2 h o ặ c m = - 3 - 2 2 .
D. m = - 3 + 2 2
Chọn C
Ta có y ' = 3 x 2 - 6 m x + 3 ( m 2 - 1 )
Hàm số (1) có cực trị thì PT y ' = 0 có 2 nghiệm phân biệt
⇔ x 2 - 2 m x + m 2 - 1 = 0 có 2 nhiệm phân biệt
![]()
Khi đó, điểm cực đại A ( m - 1 ; 2 - 2 m ) và điểm cực tiểu B ( m + 1 ; - 2 m )
Ta có O A = 2 O B ⇔ m 2 + 6 m + 1 = 0
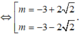
Cho hàm số : \(y=x^3-3mx^2+3\left(m^2-1\right)x-m^3+m\left(1\right)\)
Tìm m để hàm số (1) có cực trị đồng thời khoảng cách từ điểm cực đại của đồ thị hàm số đến góc tọa độ O bằng \(\sqrt{2}\) lần khoảng cách từ cực tiểu của đồ thị hàm số đến góc tọa độ O
Ta có : \(y'=3x^2-6mx+3\left(m^2-1\right)\)
Để hàm số có cực trị thì phương trình \(y'=0\) có 2 nghiệm phân biệt
\(\Leftrightarrow x^2-2mx+m^2-1=0\) có 2 nghiệm phân biệt
\(\Leftrightarrow\Delta=1>0\) với mọi m
Cực đại của đồ thị hàm số là A(m-1;2-2m) và cực tiểu của đồ thị hàm số là B (m+1; -2-2m)
Theo giả thiết ta có :
\(OA=\sqrt{2}OB\Leftrightarrow m^2+6m+1\Leftrightarrow\begin{cases}m=-3+2\sqrt{2}\\m=-3-2\sqrt{2}\end{cases}\)
Vậy có 2 giá trị m là \(\begin{cases}m=-3+2\sqrt{2}\\m=-3-2\sqrt{2}\end{cases}\)
cho hàm số : y=mx-2 Tìm m để đồ thị hàm số cách gốc tọa độ 1 khoảng bằng 1
Tìm m để đồ thị hàm số cách gốc tọa độ 1 khoang lớn nhất
giúp_mình_với_ạ