Cho hình chữ nhật ABCD kẻ BK vuông góc vs AC ở P gọi M, N là TĐ AK và CD kẻ CI vuông góc vs BM ở I và cắt BK ở E
1,c/m ME//NC//AB và E là TĐ KB
2,tứ giác MNCE là hình j ?
3, c/m BM vuông góc vs MN
4, cho BK =4cm AC =10cm tính SABCD
Cho hình chữ nhật ABCD, kẻ BK vuông góc AC ở K ( K thuộc AC ). Gọi M,N lần lượt là trung điểm AK, CD. Kẻ CI vuông góc BM ở I và cắt BK ở E
a, ME // NCE là trung điểm KBMNCE là hình gì BM vuông góc MNvẽ hình giúp với.
cho hình chữ nhật abcd.kẻ bk vuông với ac ở k. gọi m và n là trung điểm ak và cd.kẻ ci vuông với bm ở i và cắt bk ở e.
1)chứng minh ME//NC//AB và E là trung điểm KB.
2)tứ giác MNCE là hình gì?
3)chứng minh BM vuông góc MN.
4)cho bk =4cm,ac=10cm.tính diện tích ABCD
Cho hình chữ nhật ABCD. Kẻ BK vuông góc với AC ở K. Gọi M và N là trung điểm của AK và CD. Kẻ CT vuông góc với BM ở I và cắt BK ở E.
a) Chứng minh ME // NC //AB và E là trung điểm của KB
cho hình chữ nhật ABCD kẻ BK vuông góc với AC láy M,N lần lượt là trung điểm của AK,DC kẻ CI vuông góc với BM (I∈BM) và CI cắt BK tại E .cmr a,vẽ hình
b,EB=EK
c,tứ giác MNCE là hình bình hành
d,MN⊥BM
a: 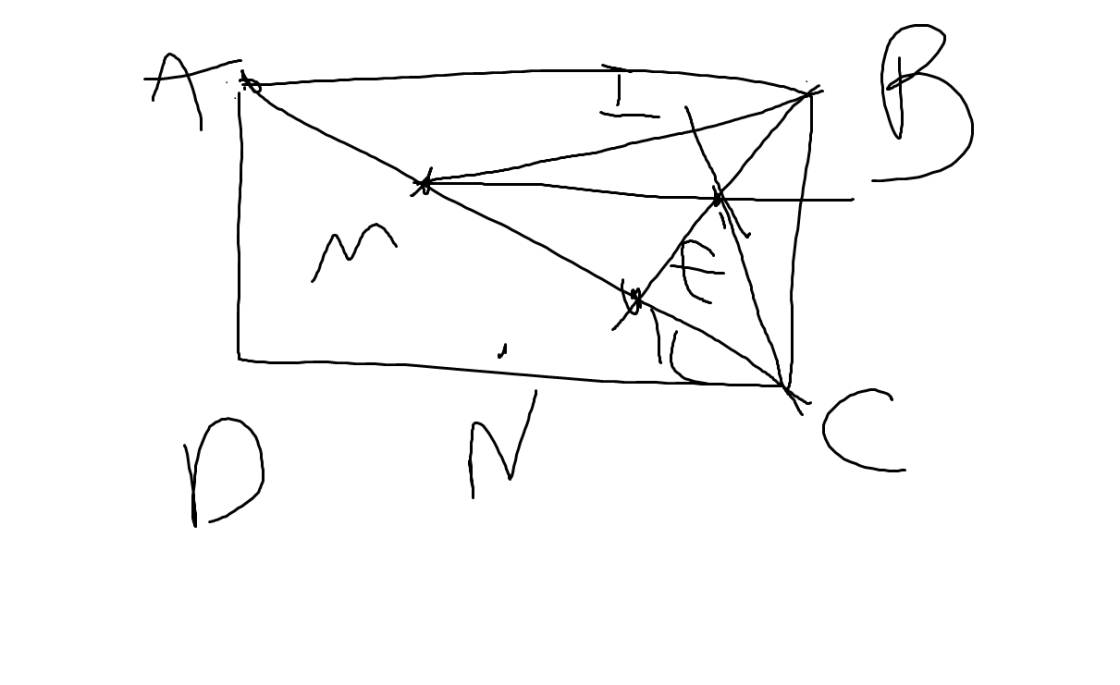
b: Xét ΔBMC có
BK,CI là các đường cao
BK cắt CI tại E
Do đó: E là trực tâm của ΔBMC
=>ME\(\perp\)BC
mà AB\(\perp\)BC
nên ME//AB
Xét ΔKAB có
M là trung điểm của KA
ME//AB
Do đó: E là trung điểm của BK
=>BE=EK
c: Xét ΔKAB có
M,E lần lượt là trung điểm của KA,KB
=>ME là đường trung bình của ΔKAB
=>\(ME=\dfrac{AB}{2}\)
mà AB=CD(ABCD là hình chữ nhật)
và \(NC=\dfrac{CD}{2}\)(N là trung điểm của CD)
nên ME=NC
Ta có: ME//AB
CD//AB
Do đó: ME//CD
Xét tứ giác MNCE có
ME//CN
ME=CN
Do đó: MNCE là hình bình hành
d: ta có: MNCE là hình bình hành
=>MN//CE
mà CE\(\perp\)MB
nên MN\(\perp\)MB
Cho hình chữ nhật ABCD.Kẻ BK vuông góc AC tại K. Gọi M và N là trung điểm AK và CD. CI vuông góc với BM ở I và cắt BK ở E.
1 Tứ giác MNCE là hình gì
2. chứng minh BM vuông góc MN
3. BK=4cm, AC=10cm. tính Diện tích ABCD
Mình cần gấp. Trước 1h45' thì càng tốt ạ
Cho hình chữ nhật ABCD. Kẻ BK vuông góc với AC ở K. Gọi M và N là trung điểm của AK và CD. Kẻ CT vuông góc với BM ở I và cắt BK ở E. CM: EB=EK
Xét ΔBNC có
CI,BK là đường cao
CI cắt BK tại E
Do đó: E là trực tâm của ΔBNC
=>NE\(\perp\)BC
mà AB\(\perp\) BC
nên NE//AB
Xét ΔKAB có
N là trung điểm của KA
NE//AB
Do đó; E là trung điểm của BK
=>EB=EK
Cho hình chữ nhật ABCD . Kẻ BP vuông góc với AC . Gọi M , N lần lượt là trung điểm của AP và CD . Kẻ CQ vuông góc với BM ở Q và cắt BP ở E .
a. Chứng minh ME vuông góc BC .
b. Tứ giác MNCE là hình gì?Vì sao?
c. Chứng minh BM vuông góc với MN
Cho hình chữ nhật ABCD . Kẻ BP vuông góc với AC . Gọi M , N lần lượt là trung điểm của AP và CD . Kẻ CQ vuông góc với BM ở Q và cắt BP ở E .
a. Chứng minh ME vuông góc BC .
b. Tứ giác MNCE là hình gì?Vì sao?
c. Chứng minh BM vuông góc với MN
a) ∆MBC có hai đường cao BP và CQ cắt nhau tại E nên E là trực tâm của tam giác => ME là đường cao thứ ba => ME⊥BC (đpcm)
b) ABCD là hình chữ nhật (1) nên AB⊥BC kết hợp với ME⊥BC => ME // AB (2) mà M là trung điểm của AP nên E là trung điểm của BP => ME là đường trung bình của ∆APB => ME = 1/2AB và NC = 1/2CD (gt) nên ME = NC (do AB = CD)
Từ (1) và (2) suy ra ME//NC
Tứ giác MNCE có ME = NC và ME//NC nên là hình bình hành
c) Tứ giác MNCE là hình bình hành nên ^NMC = ^MCE
Mà ^MCE + ^CMQ = 900 (∆MCQ vuông tại Q) nên ^NMC + ^CMQ = 900 => NMQ = 900 => BM vuông góc với MN (đpcm)
Cho hình chữ nhật ABCD . Kẻ BP vuông góc với AC . Gọi M , N lần lượt là trung điểm của AP và CD . Kẻ CQ vuông góc với BM ở Q và cắt BP ở E .
a. Chứng minh ME vuông góc BC .
b. Tứ giác MNCE là hình gì?Vì sao?
c. Chứng minh BM vuông góc với MN