cho tam giác ABC cân tại A. Tia phân giác \(\widehat{B}\)cắt AC tại D, tia phân giác \(\widehat{C}\)cắt AB vuông góc tại F . Chứng minh ADE cân
hàng quá gấp . Giúp tớ với!
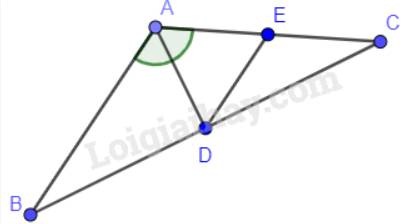
Cho tam giác ABC cân tại A (Hình 16). Tia phân giác của góc B cắt AC tại F, tia phân giác của góc C cắt AB tại E.
a) Chứng minh rẳng \(\widehat {ABF} = \widehat {ACE}\)
b) Chứng minh rằng tam giác AEF cân
c) Gọi I là giao điểm của BF và CE. Chứng minh rằng tam giác IBC và tam giác IEF là những tam giác cân
a) Vì tam giác ABC cân tại A
\( \Rightarrow \widehat B = \widehat C \Rightarrow \dfrac{1}{2}\widehat B = \dfrac{1}{2}\widehat C \Rightarrow \widehat {ABF} = \widehat {ACE}\)
b) Xét \(\Delta ECA\) và \(\Delta FBA\)có:
\(\widehat{A}\) chung
AB = AC
\(\widehat {ABF} = \widehat {ACE}\)
\( \Rightarrow \)\(\Delta ECA\)= \(\Delta FBA\)( g – c – g )
\( \Rightarrow AE = AF và EC = BF\) (2 cạnh tương ứng)
\( \Rightarrow \Delta AEF\) cân tại A
c) Xét tam giác IBC có :
\(\widehat B = \widehat C \Rightarrow \dfrac{1}{2}\widehat B = \dfrac{1}{2}\widehat C \Rightarrow \widehat {ICB} = \widehat {IBC}\)
Do đó, tam giác IBC cân tại I ( 2 góc ở đáy bằng nhau )
\( \Rightarrow IB = IC\)( cạnh tương ứng )
Vì EC = BF ( câu b) và IB = IC
\( \Rightarrow \) EC – IC = BF – BI
\( \Rightarrow \) EI = FI
\( \Rightarrow \Delta IEF\) cân tại I
Cho tam giác ABC cân tại A Tia phân giác góc B cắt cạnh AC tại D, tia phân giác góc C cắt cạnh AB tại E. Chứng minh tam giác ADE cân.
Chứng minh được tam giác ADB = tam giác AEC (g-c-g) => AD = AE, từ đó tam giác ADE cân tại A.
Cho tam giác ABC cân tại A Tia phân giác góc B cắt cạnh AC tại D, tia phân giác góc C cắt cạnh AB tại E. Chứng minh tam giác ADE cân
Cho tam giác ABC có AB < AC. Tia phân giác của góc A cắt BC tại D, trên tia AC lấy điểm E sao cho góc ADB = góc ADE.
a) Chứng minh tam giác ABE là tam giác cân.
b) Đường thẳng DE cắt tia AB tại F. Chứng minh tam giác AFC là tam giác cân.
c) Chứng minh BE // FC.
d) Qua C kẻ đường thẳng vuông góc với AC, qua F kẻ đường thẳng vuông góc với AF, hai đường thẳng này cắt nhau tại I. Chứng minh ba điểm A, D, I thẳng hàng.
cho tam giác ABC cân tại A, tia phân giác của góc B cắt cạnh AC tại D,tia phân giác của góc C cắt cạnh AB tại E
a) Chứng minh :tam giác BEC=tam giác BDC
b)Chứng minh : tam giác ADE là tam giác cân
a.TG ABC cân tại A gt
=> ^B = ^C tính chất tg cân
Mà ^ECB=^ACE=1/2^C ( CE là pg ^C)
^DBC=^ABD=1/2^B ( BD là pg ^B)
=> ^ECB=^ACE =^DBC=^ABD
Xét tg BEC và tg CDB có:
^ECB = ^DBC(cmt)
BC chung
^B=^C (tg ABC cân tại A)
=>tg BEC = tg CDB(g-c-g)
b. Xét tg ABD và tg ACE có
^A chung
AB = AC (tg ABC cân tại A)
^ABD=^ACE(cmt)
=>tg ABD = tg ACE(g-c-g)
=>AD=AE (cctu)
=> tg ADE là tg cân
Cho tam giác ABC có \(\widehat A = 120^\circ \). Tia phân giác của góc A cắt cạnh BC tại D. Đường thẳng qua D song song với AB cắt cạnh AC tại E. Chứng minh rằng tam giác ADE đều.
\(\widehat A = 120^\circ \)nên \(\widehat {DAE} = 60^\circ \)(AD là phân giác của góc A).
Ta có: DE // AB nên \(\widehat {CED} = \widehat {EAB} = 120^\circ \)(hai góc đồng vị). Ba điểm A, E, C thẳng hàng nên góc AEC bằng 180°
\(\Rightarrow \widehat {AED} = 180^\circ - \widehat {CED} = 180^\circ - 120^\circ = 60^\circ \)
Tam giác ADE có \(\widehat {EAD} = \widehat {ADE}\) (\(=60^0\)) nên là tam giác cân.
Mà \(\widehat {DEA} = 60^\circ \)
Do đó, tam giác ADE đều ( tam giác cân có 1 góc bằng \(60^0\)).
Cho tam giác ABC vuông tại A, kẻ AH vuông góc với BC tại H. Tia phân giác của \(\widehat{HAC}\) cắt BC tại D. tia phân giác của \(\widehat{HAB}\) cắt BC tại E. Kẻ EM vuông góc với AB tại M. Chứng minh rằng:
a, tam giác BME đồng dạng tam giác AHC
b, Tam giác AEC cân
c, DH.EC=AH.DC
d, AB+AC=BC+DE
Giúp mình với. Các bạn không cần vẽ hình cũng được
a) Xét 2 tam giác BME và tam giác AHC
có \(\widehat{BME}=\widehat{AHC}=90^0\)
\(\widehat{ABC}chung\)
nên 2 tam giác BME và tam giác AHC đồng dạng với nhau
b)
xét tam giác ABH
có AE là phân giác của góc BAH
nên \(\widehat{MAE}=\widehat{HAE}\)
có \(\widehat{MAE}+\widehat{CAE}=90^0\)
\(\widehat{HAE}+\widehat{CEA}=90^0\)
suy ra \(\widehat{CAE}=\widehat{CEA}\)do đó tam giác AEc cân tại C
c)
xét tam giác AHC có
AD là tia phân giác của góc HAC
nên \(\frac{HD}{CD}=\frac{AH}{AC}\Rightarrow AH\cdot CD=DH\cdot AC\)
lại có AC = EC
nên \(AH\cdot CD=EC\cdot AC\)
d)
chứng minh tương tự câu b
ta có tam giác ABD cân tại B
suy ra AB = BD
mà AC = EC
nên AB + AC = BD + EC = BD + CD + ED = BC + DE
Cho tam giác ABC có AH vuông góc với BC, có góc BAH = 2\(\widehat{C}\) Tia phân giác của \(\widehat{B}\) cắt AC tại E
a. Tia phân giác của \(\widehat{BAH}\) cắt BE tại I. Chứng minh tam giác AIE vuông cân
b. Chứng minh HE là phân giác của \(\widehat{HAC}\)
Cho \(\Delta ABC\) có \(\widehat{B}\) và \(\widehat{C}\). Vẽ tia phân giác \(\widehat{B}\) cắt AC tại D, vẽ tia phân giác \(\widehat{C}\) cắt AB tại E, BD cắt CE tại F. Chứng minh rằng:
a) BD = CE
b) \(\Delta BEF=\Delta CDF\)
c) AF là tia phân giác của \(\widehat{BAC}\)