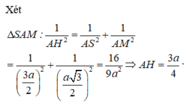cho hình thoi ABCD, gọi M;N;P;Q lần lượt là trung điểm của các cạnh AB,BC,CD,DA
a.chứng minh bốn điểm M;N;P;Q thuộc đường tròn tâm O
b. tìm điều kiện của hình thoi để các đỉnh B; D cũng thuộc đường tròn tâm O

Những câu hỏi liên quan
Bài 12: Cho hình thoi ABCD có AH là đường cao. Gọi M là trung điểm của AD . Biết a) Chứng minh: HM = AM b) Chứng minh: Tam giác AHM đều c) Tính số đo các góc của hình thoi ABCD.
Cho hình thang cân ABCD , gọi M , N , P , Q lần lượt là trung điểm của AB , BC , CD , AC .
a. Chứng minh tứ giác MNPQ là hình thoi .
b. Cho AC = 16 cm , BD = 30 cm . Tính chu vi hình thoi ABCD
Cho hình thang cân ABCD , gọi M , N , P , Q lần lượt là trung điểm của AB , BC , CD , AC .
a. Chứng minh tứ giác MNPQ là hình thoi .
b. Cho AC = 16 cm , BD = 30 cm . Tính chu vi hình thoi ABCD
Cho hình thang cân ABCD , gọi M , N , P , Q lần lượt là trung điểm của AB , BC , CD , AC .
a. Chứng minh tứ giác MNPQ là hình thoi .
b. Cho AC = 16 cm , BD = 30 cm . Tính chu vi hình thoi ABCD
Cho hình thang cân ABCD , gọi M , N , P , Q lần lượt là trung điểm của AB , BC , CD , AC .
a. Chứng minh tứ giác MNPQ là hình thoi .
b. Cho AC = 16 cm , BD = 30 cm . Tính chu vi hình thoi ABCD
Cho hình thang cân ABCD , gọi M , N , P , Q lần lượt là trung điểm của AB , BC , CD , AC .
a. Chứng minh tứ giác MNPQ là hình thoi .
b. Cho AC = 16 cm , BD = 30 cm . Tính chu vi hình thoi ABCD
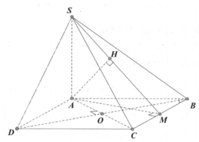
Cho hình chóp S.ABCD có ABCD là hình thoi cạnh a,
A
B
C
⏜
60
°
,
S
A
⊥
A
B
C
D
,
S
A
3
a
2
. Gọi O là tâm hình thoi ABCD. Khoảng cách từ điểm O đến (SBC) ...
Đọc tiếp
Cho hình chóp S.ABCD có ABCD là hình thoi cạnh a,
A B C ⏜ = 60 ° , S A ⊥ A B C D , S A = 3 a 2 . Gọi O là tâm hình thoi ABCD. Khoảng cách từ điểm O đến (SBC) bằng
A. 3 a 4
B. 3 a 8 .
C. 5 a 8
D. 5 a 4 .
Cho hình chóp S.ABCD có ABCD là hình thoi cạnh a,
A
B
C
^
60
ο
, SA
⊥
(ABCD), SA
3
a
2
. Gọi O là tâm hình thoi ABCD. Khoảng cách từ điểm O đến (SBC) bằng
Đọc tiếp
Cho hình chóp S.ABCD có ABCD là hình thoi cạnh a, A B C ^ = 60 ο ,
SA ⊥ (ABCD), SA= 3 a 2 . Gọi O là tâm hình thoi ABCD. Khoảng cách
từ điểm O đến (SBC) bằng
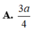
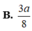
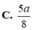
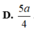
Cho hình thoi ABCD. Gọi M, N, P, Q lần lượt là trung điểm AB, BC, AC, AD. 1) Chứng minh MN=PQ 2) Chứng minh MN ⊥ MQ 3) Chứng minh MNPQ là hình chữ nhật 4) Chứng minh MBPD là hình bình hành, suy ra M, O, P thẳng hàng (O là tâm hình thoi ABCD)
a: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của BC
Do đó: MN là đường trung bình
=>MN=AC/2(1)
Xét ΔADC có
Q là trung điểm của AD
P là trung điểm của CD
Do đó: QP là đường trung bình của ΔADC
Suy ra: QP//AC và QP=AC/2(2)
Từ (1) và (2) suy ra MN=QP
Đúng 1
Bình luận (0)
Cho hình thoi ABCD. Gọi O là giao điểm của hai đường chéo, biết AB = 5cm và AO = 3cm. Diện tích hình thoi ABCD là:
A. 12 c m 2
B. 24 c m 2
C. 36 c m 2
D. 48 c m 2