chung minh rang fx chia het cho gx voi fx x 99 x 88 x 77 ... x 11 1và g x x 9 x 8 ... x 1

Những câu hỏi liên quan
chung minh rang fx chia het cho gx voi fx=x^99+x^88+x^77+...+x^11+1và g(x)=x^9+x^8+...+x+1
cho f(x)=x99+x88+x77+...+x11+1
cho g(x)=x9+x8+...+x+1
chứng minh f(x) chia hết g(x)
Ta có:
\(f\left(x\right)=x^{99}+x^{88}+x^{77}+...+x^{11}+1\)
\(f\left(x\right)=\left(x^{99}+x^{88}+x^{77}+...+x^{11}\right)+1\)
\(f\left(x\right)=\left[\left(x^9\right)^{11}+\left(x^8\right)^{11}+\left(x^7\right)^{11}+...+x^{11}\right]+1\)
Ta thấy:
\(\left(x^9\right)^{11}\) chia hết cho \(x^9\)
\(\left(x^8\right)^{11}\) chia hết cho \(x^8\)
\(..........\)
\(x^{11}\) chia hết cho \(x\)
\(1\) chia hết cho \(1\)
\(\Rightarrow f\left(x\right)\) chia hết cho \(g\left(x\right)\) ( Đpcm )
Đúng 0
Bình luận (0)
Chứng minh rằng f(x) chia hết cho g(x) với :
f(x) = x99 + x88 + x77 + ... + x11 + 1 ;
g(x) = x9 + x8 + x7 + ... + x + 1 .
CMR: f(x) chia hết cho g(x) với:
\(f\left(x\right)=x^{99}+x^{88}+x^{77}+...+x^{11}+1\)
\(g\left(x\right)=x^9+x^8+x^7+...+x+1\)
CMR: f(x) chia hết cho g(x) với:
\(f\left(x\right)=x^{99}+x^{88}+x^{77}+...+x^{11}+1\)
\(g\left(x\right)=x^9+x^8+x^7+...+x+1\)
Chứng minh rằng f(x) chia hết cho g(x) với :
\(f\left(x\right)=x^{99}+x^{88}+x^{77}+....+x+1\)
\(g\left(x\right)=x^9+x^8+x^7+....+x+1\)
Sửa lại đề bài nhé . \(f\left(x\right)=x^{99}+x^{88}+x^{77}+...+x^{11}+1\)
Xét hiệu \(f\left(x\right)-g\left(x\right)=x^9\left(x^{90}-1\right)+x^8\left(x^{80}-1\right)+x^7\left(x^{70}-1\right)+...+x\left(x^{10}-1\right)\)
\(=x^9\left[\left(x^{10}\right)^9-1\right]+x^8\left[\left(x^{10}\right)^8-1\right]+x^7\left[\left(x^{10}\right)^7-1\right]+...+x\left(x^{10}-1\right)\)
\(\Rightarrow f\left(x\right)-g\left(x\right)⋮\left(x^{10}-1\right)\)
Mà \(x^{10}-1=\left(x-1\right)\left(x^9+x^8+x^7+...+x+1\right)\)
\(\Rightarrow f\left(x\right)-g\left(x\right)⋮g\left(x\right)\Rightarrow f\left(x\right)⋮g\left(x\right)\)
Chúc bạn học tốt
Đúng 0
Bình luận (0)
cho f(x)=x^99+x^88+...+x^11+x và g(x)=x^9+x^8+...+x+1.CMR: f(x) chia hết cho g(x)
Chứng minh: \(f\left(x\right)⋮g\left(x\right)\) biết: \(f\left(x\right)=x^{99}+x^{88}+x^{77}+.............+x^{11}+1\)
\(g\left(x\right)=x^9+x^8+x^7+..............+x+1\)
Cho hàm số
f
x
m
x
4
+
n
x
3
+
p
x
2
+
q
x
+
r
m
≠
0
. Chia
f
x
cho
x
-
2
được phần dư bằng 2019, chia
f...
Đọc tiếp
Cho hàm số f x = m x 4 + n x 3 + p x 2 + q x + r m ≠ 0 . Chia f x cho x - 2 được phần dư bằng 2019, chia f ' x cho x - 2 được phần dư bằng 2018. Gọi g x là phần dư khi chia f x cho x - 2 2 . Giá trị của g - 1 là
A. - 4033
B. - 4035
C. - 4039
D. - 4037
Do f x chi cho x - 2 được phần dư là 2019 nên ta viết lại:
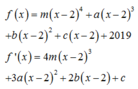
Do f ' x chi cho x - 2 dư 2018 nên c = 2018 .
Suy ra
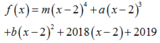
Từ đó phần dư khi chia
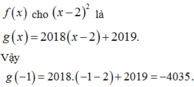
Chọn B.
Đúng 0
Bình luận (0)














