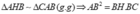cho tam giác abc vuông tại a đường cao ah chứng minh rằng 2√bh.hc ≤ bc

Những câu hỏi liên quan
Cho tam giác ABC vuông tại A, BC = a, đường cao AH.
a, Chứng minh rằng: AH=a sinBcosB; BH = a cos^2B ; CH = a sin^2 B
b, Suy ra AB^2 = BC.BH ; AH^2 = BH.HC
Ban chua hoc He thuc luong trong tam giac vuong va sin,cos ak ?
Đúng 0
Bình luận (0)
Neu hoc roi thi chi can tu suy luan qua tam giac dong dang va cac ti so lien quan la xong
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, kẻ Đường cao AH
Chứng minh: AH^2 =BH.HC
Cho tam giác ABC. Kẻ AH vuông góc với BC ( H nằm giữa B và C ) và có AH2=BH.HC. Chứng minh rằng tam giác ABC vuông tại A
Cho tam giác ABC vuông tại A, đường cao AH. Chứng minh
a) A B 2 = B H . B C ;
b) A H 2 = B H . H C .
Cho tam giác ABC vuông tại A, có AB =6cm;AC=8cm , BC=10cm.Đường cao AH(H thuộc BC)
a) Chỉ ra các cặp tam giác đồng dạng
b) Cho AD là đường phân giác của tam giác ABC (D thuộc BC) . Tính độ dài DB và DC
c) Chứng minh rằng BH.HC=AH bình
help thank
a, dễ mà dài, bạn tự làm nhé
b, Vì AD là đường pg của tam giác ABC nên
\(\frac{AC}{AB}=\frac{CD}{BD}\)( tính chất )
mà \(BD=BC-CD=10-CD\)(*)
\(\Rightarrow\frac{8}{6}=\frac{CD}{10-CD}\Rightarrow CD=\frac{40}{7}\)cm
Theo (*) suy ra : \(BD=10-\frac{40}{7}=\frac{30}{7}\)cm
cho tam giác abc vuông tại a đường cao ah ac=3 bc=5 kẻ cx vgoc vs ac tại c tia cx cắt ah tại d chứng minh ah.hd+bh.hc=ac^2
mọi người giúp mình zới
ΔCAD vuông tại C có CH là đường cao
nên AH*HD=CH^2
ΔABC vuông tại A có AH là đường cao
nên BH*HC=AH^2
AH*HD+BH*HC=CH^2+AH^2=CA^2
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A có đường cao AH, kẻ tia Bx song song với AC sao cho tia AH cắt tia Bx tại D.
Biết AB=15cm,BC=25cm.Tính BH,HAChứng Minh BH.HC=AH.ADChứng minh rằng Cos2 C=CH trên CBCho tam giác ABC vuông tại A. Đường cao AH.
1.Chứng minh tam giác ABC đồng dang với tam giác Hac.Từ đó suy ra AC^2CH.BC
2.Chứng minh AH^2BH.HC
3. Kẻ phân giác BE của tam giác ABC,phân giác EM của tam giác AEB, phân giác En của tam giác BEC. Chứng minh: dfrac{BM}{MA}.dfrac{EA}{EC}.dfrac{CN}{BN}1
Đọc tiếp
Cho tam giác ABC vuông tại A. Đường cao AH.
1.Chứng minh tam giác ABC đồng dang với tam giác Hac.Từ đó suy ra AC\(^2\)=CH.BC
2.Chứng minh AH\(^2\)=BH.HC
3. Kẻ phân giác BE của tam giác ABC,phân giác EM của tam giác AEB, phân giác En của tam giác BEC. Chứng minh: \(\dfrac{BM}{MA}\).\(\dfrac{EA}{EC}\).\(\dfrac{CN}{BN}\)=1
Cho tam giác ABC vuông ở A, đường cao AH. Chứng minh rằng:a) Tam giác ABC đồng dạng với tam giác HBA;b) AB BH.BC 2 ;c) AH BH.HC 2 .
Đọc tiếp
Cho tam giác ABC vuông ở A, đường cao AH. Chứng minh rằng:
a) Tam giác ABC đồng dạng với tam giác HBA;
b) AB BH.BC 2 ;
c) AH BH.HC 2 .
a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
=>ΔABC đồng dạng với ΔHBA
b: ΔBAC đồng dạng với ΔBHA
=>BA/BH=BC/BA
=>BA^2=BH*BC
c: Xét ΔHAC vuông tại H và ΔHBA vuông tại H có
góc HAC=góc HBA
=>ΔHAC đồng dạng với ΔHBA
=>HA/HB=HC/HA
=>HA^2=HB*HC
Đúng 0
Bình luận (1)