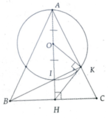
a, Chứng minh được  B K A ^ = 90 0

b, Gọi O là trung điểm AI

Ta có:

+ OK = OA =>  O K A ^ = O A K ^

+  O A K ^ = H B K ^ (cùng phụ  A C B ^ )

+ HB = HK =>  H B K ^ = H K B ^

=> O K A ^ = H K B ^ ⇒ H K O ^ = 90 0

a: Vì góc AKI=90 độ

nên K nằm trên đường tròn đường kính AI

b: Gọi G là trung điểm của AK

góc GKH=góc GKI+góc HKI

=góc GIK+góc HBI

=góc BIH+góc HBI=90 độ

=>HK là tiếp tuyến của (G)

Đáp án A

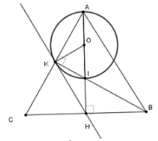
Gọi O là trung điểm AI. Xét tam giác vuông AIK có

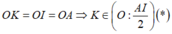
Xét tam giác OKA cân tại O (vì OA=OK=R) có:

O K A ^ = O A K ^  (1)

Xét tam giác CKB vuông tại K (vì  K B ⊥ A C ) có:

H là trung điểm CB (vì tam giác ABC cân tại A có AH là đường cao nên đồng thời là đường trung tuyến)

⇒ KH là trung tuyến ứng với cạnh huyền BC

⇒ H K C ^ = H C K ^   ( 2 )

Từ (1) và (2) suy ra  O K A ^ + H K C ^ = O A K ^ + H C K ^ = 90 o (vì  A H ⊥ B C )

Mà  O K A ^ + H K C ^ + O K H ^ = 180 o ⇒ O K H ^ = 90 o ⇒ O K ⊥ K H (**)

Từ (*) và (**) suy ra HK là tiếp tuyến của (O)

Chọn đáp án A

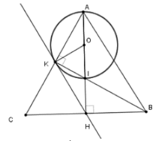
Gọi O là trung điểm AI. Xét tam giác vuông AIK có

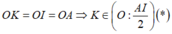
Từ (*) và (**) thì HK là tiếp tuyến của đường tròn đường kính AI

a: Ta có: ΔBKC vuông tại K

mà KH là trung tuyến

nên KH=BH

=>ΔHBK cân tại H

b: góc BAH=90 độ-góc ABC

góc IAK=90 độ-góc ACB

mà góc ABC=góc ACB

nên góc BAH=góc IAK

c: Gọi G là trung điểm của AI

góc GKH=góc GKI+góc HKI

=góc GIK+góc HBI

=góc BIH+góc HBI=90 độ

=>HK là tiếp tuyến của (G)

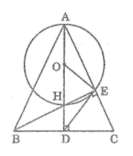
Ta có : OH = OE

Suy ra tam giác OHE cân tại O

Trong tam giác BDH ta có:

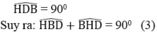
Từ (1), (2) và (3) suy ra:

Tam giác ABC cân tại A có AD ⊥ BC nên BD = CD

Tam giác BCE vuông tại E có ED là đường trung tuyến nên:

ED = DB = BC/2 (tính chất tam giác vuông)

Suy ra tam giác BDE cân tại D

Suy ra: DE ⊥ EO. Vậy DE là tiếp tuyến của đường tròn (O).