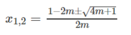Giải và biện luận phương trình theo tham số m, n.
m(x-3)+2(x-n)=3-x
Bài 1: Giải và biện luận các phương trình sau theo tham số m a) 2mx + 3 = m - x b) m(x - 2) = 3x + 1
b: Để phương trình vô nghiệm thì x-2=0
hay x=2
Để phương trình có nghiệm thì x-2<>0
hay x<>2
Giải và biện luận các phương trình sau theo tham số m
a, m(x-m+3)=m(x-2)+6
b, (m+1)x^2 - 2(m-1)x+ m -2=0
a: \(\Leftrightarrow mx-m^2+3m=mx-2m+6\)
\(\Leftrightarrow-m^2+5m-6=0\)
\(\Leftrightarrow\left(m-2\right)\left(m-3\right)=0\)
=>m=2 hoặc ,=3
b: Để phương trình là phương trình bậc hai một ẩn thì m+1<>0
hay m<>-1
\(\text{Δ}=\left(2m-2\right)^2-4\left(m+1\right)\left(m-2\right)\)
\(=4m^2-8m+4-4\left(m^2-m-2\right)\)
\(=4m^2-8m+4-4m^2+4m+8\)
=-4m+12
Để phương trình có hai nghiệm phân biệt thì -4m+12>0
=>-4m>-12
hay m<3
Để phương trình có nghiệm kép thì -4m+12=0
hay m=3
Để phương trình vô nghiệm thì -4m+12<0
hay m>3
Giải và biện luận phương trình sau theo tham số m: m(x – 4) = 5x – 2.
m(x – 4) = 5x – 2 ⇔(m - 5)x = 4m - 2
Nếu m - 5 ≠ 0 ⇔ m ≠ 5 thì phương trình có nghiệm duy nhất
x = (4m - 2)/(m - 5)
Nếu m – 5 = 0 ⇔ m = 5, phương trình trở thành:
0.x = 18 ⇒ phương trình vô nghiệm
Vậy với m ≠ 5 phương trình có nghiệm duy nhất
x = (4m - 2)/(m - 5)
Với m = 5 phương trình vô nghiệm.
Phương trình tương đương
\(\left\{{}\begin{matrix}\left(m-1\right)x+2=\left(m+1\right)\left(x-2\right)\\x\ne2\end{matrix}\right.\)
⇔ \(\left\{{}\begin{matrix}\left(m-1\right)x+2=\left(m+1\right)x-2m-2\\x\ne2\end{matrix}\right.\)
⇔ \(\left\{{}\begin{matrix}\left(m-1-m-1\right)x=-2m-4\\x\ne2\end{matrix}\right.\)
⇔ \(\left\{{}\begin{matrix}-2x=-2m-4\\x\ne2\end{matrix}\right.\)
⇔ \(\left\{{}\begin{matrix}x=m+2\\x\ne2\end{matrix}\right.\)
Nếu m = 0 thì phương trình vô nghiệm
Nếu m ≠ 0 thì S = {m + 2}
Giải và biện luận theo tham số m các phương trình sau
2 x + m = x - 2 m + 2
![]()
Phương trình (1) ⇔ x = -3m + 2
Phương trình (2) ⇔ 3x = m - 2 ⇔ x = (m - 2) / 3
Vậy với mọi giá trị của m phương trình có nghiệm là:
x 1 = -3m + 2 và x 2 = (m - 2) / 3
Giải và biện luận các phương trình sau theo tham số m: m(x - 2) = 3x + 1
m(x – 2) = 3x + 1
⇔ mx – 2m = 3x + 1
⇔ mx – 3x = 1 + 2m
⇔ (m – 3).x = 1 + 2m (1)
+ Xét m – 3 ≠ 0 ⇔ m ≠ 3, phương trình (1) có nghiệm duy nhất 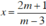
+ Xét m – 3 = 0 ⇔ m = 3, pt (1) ⇔ 0x = 7. Phương trình vô nghiệm.
Kết luận:
+ với m = 3, phương trình vô nghiệm
+ với m ≠ 3, phương trình có nghiệm duy nhất 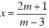
Cho phương trình (m+2)x2−2(m−1)x+3−m=0 (1); với m là tham số thực
1) Giải và biện luận phương trình đã cho theo tham số m
2) Tìm m để phương (1) có hai nghiệm thỏa mãn tổng hai nghiệm bằng tích hai nghiệm.
1: Ta có: \(\text{Δ}=\left[-2\left(m-1\right)\right]^2-4\cdot\left(m+2\right)\left(3-m\right)\)
\(=\left(2m-2\right)^2+4\left(m+2\right)\left(m-3\right)\)
\(=4m^2-8m+4+4\left(m^2-3m+2m-6\right)\)
\(=4m^2-8m+4+4m^2-4m-24\)
\(=-12m-20\)
Để phương trình có hai nghiệm phân biệt thì Δ>0
\(\Leftrightarrow-12m-20>0\)
\(\Leftrightarrow-12m>20\)
hay \(m< \dfrac{-5}{3}\)
Để phương trình có nghiệm kép thì Δ=0
\(\Leftrightarrow-12m-20=0\)
\(\Leftrightarrow-12m=20\)
hay \(m=\dfrac{-5}{3}\)
Để phương trình vô nghiệm thì Δ<0
\(\Leftrightarrow-12m-20< 0\)
\(\Leftrightarrow-12m< 20\)
hay \(m>\dfrac{-5}{3}\)
2: ĐKXĐ: \(m\ne-2\)
Áp dụng hệ thức Vi-et, ta được:
\(\left\{{}\begin{matrix}x_1+x_2=\dfrac{2\left(m-1\right)}{m+2}=\dfrac{2m-2}{m+2}\\x_1\cdot x_2=\dfrac{3-m}{m+2}\end{matrix}\right.\)
Ta có: \(x_1+x_2=x_1x_2\)
\(\Leftrightarrow\dfrac{2m-2}{m+2}=\dfrac{3-m}{m+2}\)
Suy ra: 2m-2=3-m
\(\Leftrightarrow2m+m=3+2\)
\(\Leftrightarrow3m=5\)
hay \(m=\dfrac{5}{3}\)(thỏa ĐK)
Bài 2: Giải và biện luận bất phương trình: \(m\left(x-m\right)\le4x+5\) theo tham số m
\(m\left(x-m\right)\le4x+5.\left(1\right)\\ \Leftrightarrow mx-m^2-4x-5\le0.\\ \Leftrightarrow\left(m-4\right)x\le5+m^2.\circledast\)
+) Nếu \(m-4>0.\Leftrightarrow m>4.\)
Khi \(\circledast\) có nghiệm: \(x\le\dfrac{5+m^2}{m-4}.\)
+) Nếu \(m-4< 0.\Leftrightarrow m< 4.\)
Khi \(\circledast\) có nghiệm: \(x\ge\dfrac{5+m^2}{m-4}.\)
+) Nếu \(m-4=0.\) \(\Leftrightarrow m=4.\)
Thay vào \(\circledast\) ta có:
\(0x\le5+4^2.\Leftrightarrow0x\le21\) (vô lý).
Kết luận:
Với \(m>4\) thì (1) có tập nghiệm \(S=\) \((-\infty;\dfrac{5+m^2}{m-4}].\)
Với \(m< 4\) thì (1) có tập nghiệm \(S=\) \([\dfrac{5+m^2}{m-4};+\infty).\)
Với \(m=4\) thì (1) có tập nghiệm \(S=\) \(\phi.\)
Giải và biện luận theo tham số m các phương trình sau
m x 2 + ( 2 m - 1 ) x + m - 2 = 0
m = 0 phương trình trở thành
-x - 2 = 0 ⇒ x = -2
m ≠ 0 phương trình đã cho là phương trình bậc hai, có Δ = 4m + 1
Với m < -1/4 phương trình vô nghiệm;
Với m ≥ -1/4 nghiệm của phương trình là