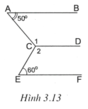
Đặt A C E ^ = m °  thì C 2 ^ = m ° + 10 °  và C 1 ^ = m ° + 20 ° .

Ta có A C E ^ + C 1 ^ + C 2 ^ = 360 °  do đó

m ° + m ° + 10 ° + m ° + 20 ° = 360 ° ⇒ 3 m ° + 30 ° = 360 ° ⇒ m ° = 110 ° .

Vậy C 2 ^ = 120 ° ; C 1 ^ = 130 ° .

Ta có A ^ + C 1 ^ = 50 ° + 130 ° = 180 ° ⇒ A B / / C D ; E ^ + C 2 ^ = 60 ° + 120 ° = 180 ° ⇒ C D / / E F ; vì có cặp góc trong cùng phía bù nhau.

Ÿ Vận dụng nhiều dấu hiệu song song

BAD + ADC = 180⁰

mà 2 góc này ở vị trí trong cùng phía

=> AB // CD

mà AB _I_ BC

=> CD _I_ BC

AB // CD

=> BAC = ACD (2 góc so le trong)

mà ACD = 40⁰

=> BAC = 40⁰

BAD + ADC = 180⁰

120⁰ + ADC = 180⁰

ADC = 180⁰ - 120⁰

ADC = 60⁰

Bài mình làm cực chi tiết nên có một số chỗ viết tắt: gt:giả thiết,  dhnb:dấu hiệu nhận biết,   đ/n:định nghĩa,   cmt:chứng minh trên,   t/c: tính chất

3. a) Vì tam giác ABC vuông cân ở A (gt)=> góc ACB=45 độ.

         tam giác ACE vuông cân ở E (gt)=> góc EAC=45 độ.

mà góc EAC và góc ACB ở vị trí so le trong.

Từ 3 điều trên=> AE//BC (dhnb) => AECB là hình thang (đ/n) mà góc AEC=90 độ (tam giác ACE vuông cân) => AECB là hình thang vuông.

b) Vì AECB là hình thàng vuông(cmt) mà góc AEC= 90 độ (tam giác ACE vuông cân). => góc ACE=90 độ.

Có: góc ABC= 45 độ (cmt).

tam giác AEC vuông cân ở E (gt)=> góc EAC=45 độ (t/c) mà góc BAC+ góc EAC= góc BAE và góc BAC= 90 độ (tam giác BAC vuông cân)=> góc BAE= 90 độ=45 độ= 135 độ.

Gọi AD là đường trung trực tam giác ABC=> AD=BD=BC=1/2BC=1/2*2=1 cm (chỗ này là tính chất tam giác vuông: trung tuyến ứng với                                                                                 cạnh huyền thì bằng nửa cạnh huyền nhé). [đây là điều thứ nhất suy ra được]

                                                                         => AD vông góc với BC. [đây là điều thứu hai suy ra được]

Xét tam giác ADC vuông tại D (AD vuông góc BC) và tam giác AEC vuông tại E (gt) có: Cạnh huyền AC chung. Góc EAC= góc BCA (cmt) => tam giác ADC= tam giác CEA (ch-gn) => AD= EC ( 2 cạnh tương ứng) mà AD=1cm(cmt) => AE=1cm.

Xét  tam giác ADB vuông (AD vuông góc BC) có: AD²+ BD² = AB² ( định lí Pytago)

                                                                                       1²   +  1²    =AB^{2 =>} 1+1=AB² => Ab bằng căn bậc hai cm.

QUỲNH LỚP 7C TRƯỜNG VÕ NGUYÊN GIẤP HẢ

ghi cả cách làm nha bạn

ghi cả cách làm luôn nha bạn

V ảnh đâu ah.

Ta cóBDA+ADC=BDC 10\(^o\)+50\(^o\)=60\(^o\)

Xét tam giác ADCvuông tại C:

\(AC=CD.tanADC\)

\(\Rightarrow AC=40.tan50^o\)

\(\Leftrightarrow AC\approx47,67cm\)

Xét tam giác BDC vuông tại C có:

\(CB=CD.\tan BDC\)

\(\Rightarrow CB=40.tan60^o\)

\(\Leftrightarrow CB\approx69,28cm\)

Ta có \(AB=BC-AC=69,28-47,67=21,61cm\)