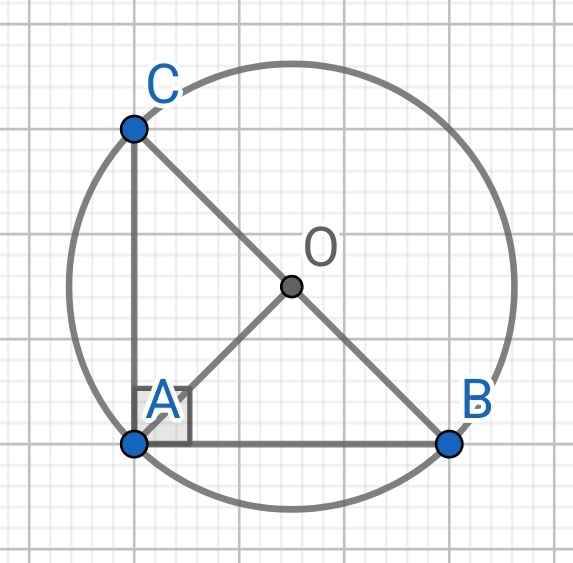
∆ABC vuông tại A

⇒ BC² = AB² + AC² (Pytago)

= a² + a²

= 2a²

⇒ BC = a√2

Tâm của đường tròn ngoại tiếp ∆ABC là trung điểm của BC

Gọi O là trung điểm của BC khi đó bán kính là OA

⇒ OA = BC/2 = a√2/2

do tam giác vuông cân nội tiếp đường tròn => đường kính = độ dài cạnh huyền của tam giác vuông cân

bình phương cạnh huyền = tổng bình phương 2 cạnh góc vuông

=> bình phương cạnh huyền = 18

=> độ dài cạnh huyền = đường kính = \(3\sqrt{2}\)

=> bán kính = \(\frac{3\sqrt{2}}{2}\)

a: Bán kính là \(\dfrac{c}{2}\)

b: Bán kính là \(\dfrac{a\sqrt{2}}{2}\)

\(h=\sqrt{b^2-\frac{a^2}{4}}\Rightarrow S=\frac{1}{2}ah=\frac{1}{2}a\sqrt{b^2-\frac{a^2}{4}}\)

\(R=\frac{abb}{4S}=\frac{ab^2}{\sqrt{4b^2-a^2}.a}=\frac{b^2}{\sqrt{4b^2-a^2}}\)

\(r=\frac{S}{p}=\frac{a\sqrt{b^2-\frac{a^2}{4}}}{a+2b}\)

trong tgiac vuông tâm đường tròn ngoại tiếp chính là trung điểm cạnh huyền

Áp dụng định lý pytago vào tgiac vuông ABC ta có :

\(BC^2\)=\(AC^2\)+\(AB^2\)

\(BC^2\)=\(8^2\)+\(6^2\)

\(BC^2\)=100

BC=10 

Vậy bán kính đường tròn ngoại tiếp tgiac ABC là:

10:2=5cm

bán kính đường tròn nội tiếp = 1 ok ;)

Gọi bk ngoại tiếp là R còn nôi tiếp là r ;p là 1/2 chu vi (= a+b+c/2)

ra có R=BC/2=5

mà S=pr=(6+8+10)/2r=6*8/2=>r=2