cho hình chữ nhật ABCD, AH vuông góc với BD (H thuộc BD), HD = 2cm, HB = 6cm. tính dộ dài AB, AD
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6

Những câu hỏi liên quan
Cho hình chữ nhật ABCD. Gọi H là chân đường vuông góc kẻ từ A đến BD. Biết HD = 2cm, HB = 6cm. Tính độ dài AD, AB (làm tròn đến hàng đơn vị).
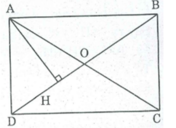
Ta có:
DB = HD + HB = 2 + 6 = 8 (cm)
AC = DB (tính chất hình chữ nhật)
OA = OB = OC = OD = 1/2 BD = 4 (cm)
OD = OH + HD
⇒ OH = OD – HD = 4 – 2 = 2 (cm)
Suy ra: OH = HD = 2 cm nên H là trung điểm của OD
Tam giác ADO có AH là đường cao đồng thời là đường trung tuyến nên tam giác ADO cân tại A
⇒AD = AO = 4 (cm)
Trong tam giác vuông ABD có ∠ (BAD) = 90 0
B D 2 = A B 2 + A D 2 (định lý Pi-ta-go) ⇒ A B 2 = B D 2 - A D 2
AB = B D 2 - A D 2 = 8 2 - 4 2 ≈ 7 (cm).
Đúng 0
Bình luận (0)
Cho hình chữ nhật ABCD. Gọi H là chân đường vuông góc kẻ từ A đến BD. Biết HD = 2cm, HB = 6cm. Tính các độ dài AD, AB .
BD = HD + HB
= 2 + 6
= 8 ( cm )
ABCD là hình chữ nhật
=> OA = OB = OC = OD = \(\frac{BD}{2}=\frac{AC}{2}=\frac{8}{2}=4\) \(\left(cm\right)\)
=> OH = OD – HD
= 4 - 2 = 2 ( cm )
\(\Delta AOD\)cân => AO = AD = 4 ( cm )
AD định lý py ta go cho tam giác ABD
BD2 = AB2 + AD2
=> AB2 = 82 - 42 = 64 - 16 = 48
=> \(AB\approx7\left(cm\right)\)
Đúng 0
Bình luận (0)
Kẻ đường chéo AC cắt BD tại O
Ta có: BD = DH + HB = 2 + 6 = 8 (cm)
\(AC=BD\Rightarrow OA=OB=OC=OD=\frac{BD}{2}=\frac{8}{2}=4\left(cm\right)\)
\(\Rightarrow OH=OD-HD=4-2=2\left(cm\right)\Rightarrow OH=HD\left(=2cm\right)\)
=> AH là đường trung tuyến của t/g OAD
Mà AH là đường cao của t/g OAD
=> t/g OAD cân tại A => OA = AD = 4 (cm)
Xét t/g ABD vuông tại A có: \(AB^2+AD^2=BD^2\) (định lí pytago)
\(\Rightarrow AB=\sqrt{BD^2-AD^2}=\sqrt{8^2-4^2}=\sqrt{48}\approx7\left(cm\right)\)
Đúng 0
Bình luận (0)
Do tứ giác ABCD là hình chữ nhật => ^BAD = 900 => ^DAH + ^HAB = 900
Mà ^HAB + ^ABH = 900 => ^DAH = ^ABH
Xét \(\Delta\)AHD và \(\Delta\)BHA: ^DAH = ^ABH; ^AHD = ^BHA (=900) => \(\Delta\)AHD ~ \(\Delta\)BHA (g.g)
=> \(\frac{AH}{BH}=\frac{DH}{AH}\Rightarrow AH^2=BH.DH=2.6=12\)
Áp dụng ĐL Pytago cho \(\Delta\)AHD vuông tại H: \(AD^2=AH^2+DH^2=12+4=16\Leftrightarrow AD=4\)
Tương tự với \(\Delta\)AHB: \(AB^2=AH^2+HB^2=12+36=48\Leftrightarrow AB=\sqrt{48}=4\sqrt{3}\)
Vậy \(AD=4;AB=4\sqrt{3}.\)
Đúng 0
Bình luận (0)
Cho hình chữ nhật ABCD. Gọi H là chân đường vuông góc kẻ từ A đến BD. Biết HD = 2cm, HB = 6cm.
Tính các độ dài AD, AB (làm tròn đến hàng đơn vị)
Cho hình chữ nhật ABCD, gọi H là chân đường vuông góc hạ từ A xuống BD( AH vuông góc với BD) . Biết HB=9cm, HD=3cm.
Tính độ dài AB, AD
hình chữ nhật ABCD có AB=8cm AD=6cm kẻ AH vuông góc BD (H thuộc BD)
a) CM tam giác HDA đồng dạng tam giác ADB
b) Tính BD,AH
c) CM BC bình = DH nhân BH
Giải giúp mình cái
d)CM AH bình=HD nhân HB
Cho hình chữ nhật ABCD AB=8cm AD=6cm Tính BD Hạ AH vuông góc với (H thuộc BD) chứng minh tam giác DHA đồng dạng với tam giác DAB Tính AH
a) Áp dụng định lí Pytago vào ΔABD vuông tại A, ta được:
\(BD^2=AB^2+AD^2\)
\(\Leftrightarrow BD^2=6^2+8^2=100\)
hay BD=10(cm)
b) Xét ΔDHA vuông tại H và ΔDAB vuông tại A có
\(\widehat{ADH}\) chung
Do đó: ΔDHA\(\sim\)ΔDAB(g-g)
Đúng 1
Bình luận (0)
Cho hình chữ nhật ABCD. Gọi H là chân đường vuông góc kẻ từ A đến BD. Biết rằng HD = 6cm, HB = 24cm. Tính các độ dài AD, AB (làm tròn đến 1 chữ số thập phân).
Cho hình chữ nhật ABCD có cạnh AB=12cm và cạnh AD=9cm. Gọi H là chân đường vuông góc kẻ từ A đến cạnh BD.
a) Chứng tỏ tam giác ADH đồng dạng với tam giác BDC và AD^2=HD.BD
b) Tính dộ dài HD và HB
c)Tia phân giác của góc ADB cắt AH tại F và AB tại E. Chứng tỏ FH/FA=EA/EB
Cho hình chữ nhật ABCD.Gọi H là chân đường vuông góc kẻ từ A đến BD. Biết HD=2cm,HB=6cm.Tính các độ dài AD, AB



















