Giúp vs mn ui,mình cảm ơn nhìu

Những câu hỏi liên quan
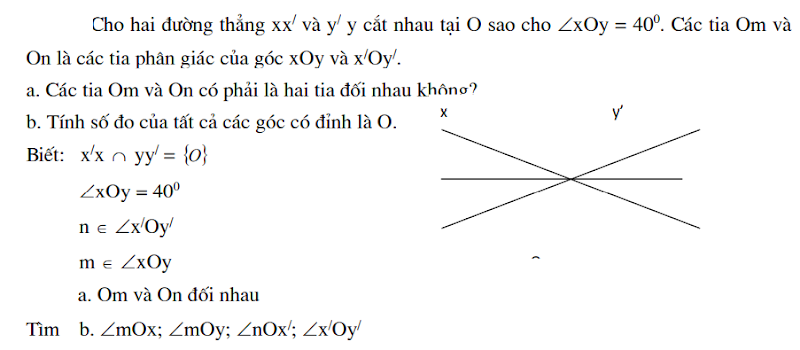 giúp mình vs nha cảm ơn mn nhìu
giúp mình vs nha cảm ơn mn nhìu
mn giải giúp mik vs ạ, giải chi tiết ra luôn, mình phải nộp trong hôm nay rùi ạ, cảm ơn mn nhìu


Bài 1:
\(a,A=6\sqrt{2}-6\sqrt{2}+2\sqrt{5}=2\sqrt{5}\\ b,B=\dfrac{\sqrt{3}\left(\sqrt{3}-1\right)}{\sqrt{3}-1}+\dfrac{\sqrt{2}\left(\sqrt{2}-1\right)}{\sqrt{2}-1}=\sqrt{3}+\sqrt{2}\\ c,=2\sqrt{3}-6\sqrt{3}+15\sqrt{3}-4\sqrt{3}=7\sqrt{3}\\ d,=1+6\sqrt{3}-\sqrt{3}-1=5\sqrt{3}\\ e,=4\sqrt{2}+\sqrt{2}-6\sqrt{2}+3\sqrt{2}=2\sqrt{2}\)
Bài 2:
\(a,ĐK:x\ge\dfrac{3}{2}\\ PT\Leftrightarrow\sqrt{2x-3}=5\Leftrightarrow2x-3=25\Leftrightarrow x=14\\ b,PT\Leftrightarrow x^2=\sqrt{\dfrac{98}{2}}=\sqrt{49}=7\Leftrightarrow\left[{}\begin{matrix}x=\sqrt{7}\\x=-\sqrt{7}\end{matrix}\right.\\ c,ĐK:x\ge3\\ PT\Leftrightarrow\sqrt{x-3}\left(\sqrt{x+3}+1\right)=0\\ \Leftrightarrow\sqrt{x-3}=0\left(\sqrt{x+3}+1>0\right)\\ \Leftrightarrow x=3\\ d,ĐK:x\ge1\\ PT\Leftrightarrow2\sqrt{x-1}-\sqrt{x-1}+3\sqrt{x-1}=4\\ \Leftrightarrow\sqrt{x-1}=1\Leftrightarrow x=2\left(tm\right)\\ e,PT\Leftrightarrow2x-1=16\Leftrightarrow x=\dfrac{17}{2}\\ f,PT\Leftrightarrow\left|2x-1\right|=\sqrt{3}-1\Leftrightarrow\left[{}\begin{matrix}2x-1=\sqrt{3}-1\\2x-1=1-\sqrt{3}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\sqrt{3}}{2}\\x=\dfrac{2-\sqrt{3}}{2}\end{matrix}\right.\)
Đúng 2
Bình luận (0)
Bài 3:
\(a,Q=\dfrac{1+5}{3-1}=3\\ b,P=\dfrac{x+\sqrt{x}-6+x-2\sqrt{x}-3-x+4\sqrt{x}+9}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\\ P=\dfrac{\sqrt{x}\left(\sqrt{x}+3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}=\dfrac{\sqrt{x}}{\sqrt{x}-3}\\ c,M=\dfrac{\sqrt{x}}{\sqrt{x}-3}\cdot\dfrac{3-\sqrt{x}}{\sqrt{x}+5}=\dfrac{-\sqrt{x}}{\sqrt{x}+5}\)
Vì \(-\sqrt{x}\le0;\sqrt{x}+5>0\) nên \(M< 0\)
Do đó \(\left|M\right|>\dfrac{1}{2}\Leftrightarrow M< -\dfrac{1}{2}\Leftrightarrow-\dfrac{\sqrt{x}}{\sqrt{x}+5}+\dfrac{1}{2}< 0\)
\(\Leftrightarrow\dfrac{2\sqrt{x}-\sqrt{x}-5}{2\left(\sqrt{x}+5\right)}< 0\Leftrightarrow\sqrt{x}-5< 0\left(\sqrt{x}+5>0\right)\\ \Leftrightarrow0\le x< 25\)
Bài 4:
\(a,A=\dfrac{16+2\cdot4+5}{4-3}=29\\ b,B=\dfrac{2\sqrt{x}-9-x+9+2x-3\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\\ B=\dfrac{x-\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}=\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}=\dfrac{\sqrt{x}+1}{\sqrt{x}-3}\\ c,P=\dfrac{x+2\sqrt{x}+5}{\sqrt{x}-3}\cdot\dfrac{\sqrt{x}-3}{\sqrt{x}+1}=\dfrac{x+2\sqrt{x}+5}{\sqrt{x}+1}\\ P=\dfrac{\left(\sqrt{x}+1\right)^2+4}{\sqrt{x}+1}=\sqrt{x}+1+\dfrac{4}{\sqrt{x}+1}\\ P\ge2\sqrt{\left(\sqrt{x}+1\right)\cdot\dfrac{4}{\sqrt{x}+1}}=2\sqrt{4}=4\\ P_{min}=4\Leftrightarrow\left(\sqrt{x}+1\right)^2=4\Leftrightarrow\sqrt{x}+1=2\Leftrightarrow x=1\left(tm\right)\)
Đúng 1
Bình luận (0)
Nhờ mn giải giúp mình PT này chi tiết một chút vs ạ, cảm ơn mn nhìu nha
(x+2)(\(\dfrac{360}{x}-6\)) = 360
\(\left(x+2\right)\left(\dfrac{360}{x}-6\right)=360\)
\(ĐK:x\ne0\)
\(\Leftrightarrow\left(x+2\right)\left(\dfrac{360-6x}{x}\right)=360\)
\(\Leftrightarrow360-6x+\dfrac{720-12x}{x}=360\)
\(\Leftrightarrow360x-6x^2+720-12x=360x\)
\(\Leftrightarrow6x^2+12x-720=0\)
\(\Delta=12^2-4.6.\left(-720\right)\)
\(=17424>0\)
`->` pt có 2 nghiệm
\(\left\{{}\begin{matrix}x_1=\dfrac{-12-\sqrt{17424}}{12}=-12\\x_2=\dfrac{-12+\sqrt{17424}}{12}=10\end{matrix}\right.\) ( tm )
Vậy \(S=\left\{-12;10\right\}\)
Đúng 2
Bình luận (0)

Mn giúp e vs ạ.E cảm ơn mn nhìu ạ
Nhờ mn giải giúp mình PT này chi tiết một chút vs ạ, cảm ơn mn nhìu nha
\(\dfrac{48}{x+4}\)+\(\dfrac{48}{x-4}\)=5
`48/[x+4]+48/[x-4]=5` `ĐK: x \ne +-4`
`<=>[48(x-4)+48(x+4)]/[(x-4)(x+4)]=[5(x+4)(x-4)]/[(x-4)(x+4)]`
`=>48x-192+48x+192=5x^2-80`
`<=>5x^2-96x-80=0`
`<=>5x^2-100+4x-80=0`
`<=>5x(x-20)+4(x-20)=0`
`<=>(x-20)(5x+4)=0`
`<=>` $\left[\begin{matrix} x=20\\ x=\dfrac{-4}{5}\end{matrix}\right.$ (t/m)
Vậy `S={-4/5;20}`
Đúng 5
Bình luận (0)
ĐK : \(x\ne\pm4\)
\(\Leftrightarrow\cdot\dfrac{48\left(x+4\right)+48\left(x-4\right)}{\left(x+4\right)\left(x-4\right)}=\dfrac{5\left(x+4\right)\left(x-4\right)}{\left(x+4\right)\left(x-4\right)}\)
\(\Leftrightarrow48x+192+48x-192==5x^2-80\)
\(\Leftrightarrow96x=5x^2-80\)
\(\Leftrightarrow5x^2-96x-80=0\)
\(\Leftrightarrow5x^2+4x-100-80=0\)
\(\Leftrightarrow4\left(x-20\right)+5x\left(x-20\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-20=0\\5x=-4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=20\\x=-\dfrac{4}{5}\end{matrix}\right.\)
Đúng 2
Bình luận (1)
Giúp mk vs , cảm ơn mn nhìu
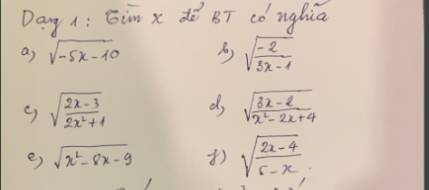
\(a,\sqrt{-5x-10}\) có nghĩa \(\Leftrightarrow-5x-10\ge0\Leftrightarrow-5x\ge10\Leftrightarrow x\le-2\)
\(b,\sqrt{\dfrac{-2}{3x-1}}\) có nghĩa \(\Leftrightarrow\dfrac{-2}{3x-1}\ge0\Leftrightarrow3x-1< 0\Leftrightarrow x< \dfrac{1}{3}\)
\(c,\sqrt{\dfrac{2x-3}{2x^2+1}}\) có nghĩa \(\Leftrightarrow\left\{{}\begin{matrix}2x-3\ge0\\2x^2+1>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x\ge3\\2x^2>-1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge\dfrac{3}{2}\\x^2>-\dfrac{1}{2}\left(loại\right)\end{matrix}\right.\)
\(\Leftrightarrow x\ge\dfrac{3}{2}\)
\(d,\sqrt{\dfrac{3x-2}{x^2-2x+4}}\) có nghĩa \(\Leftrightarrow\left\{{}\begin{matrix}3x-2\ge0\\x^2-2x+4>0\end{matrix}\right.\)
\(\Leftrightarrow3x\ge2\)
\(\Leftrightarrow x\ge\dfrac{2}{3}\)
\(e,\sqrt{x^2-8x-9}\) có nghĩa \(\Leftrightarrow x^2-8x-9\ge0\)
\(\Leftrightarrow x^2+x-9x-9\ge0\)
\(\Leftrightarrow x\left(x+1\right)-9\left(x+1\right)\ge0\)
\(\Leftrightarrow\left(x-9\right)\left(x+1\right)\ge0\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x-9\ge0\\x+1\ge0\end{matrix}\right.\\\left\{{}\begin{matrix}x-9\le0\\x+1\le0\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x\ge9\\x\ge-1\end{matrix}\right.\\\left\{{}\begin{matrix}x\le9\\x\le-1\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge9\\x\le-1\end{matrix}\right.\)
\(f,\sqrt{\dfrac{2x-4}{5-x}}\) có nghĩa \(\Leftrightarrow\left\{{}\begin{matrix}2x-4\ge0\\5-x>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge2\\x< 5\end{matrix}\right.\)
Đúng 2
Bình luận (1)
a: ĐKXĐ: -5x-10>=0
=>x<=-2
b: ĐKXĐ: 3x-1<0
=>x<1/3
c: ĐKXĐ: 2x-3>=0
=>x>=3/2
e: ĐKXĐ: (x-9)(x+1)>=0
=>x>=9 hoặc x<=-1
d: ĐKXĐ: 3x-2>=0
=>x>=2/3
Đúng 1
Bình luận (1)
Tính nhanh
23 x 58 - 30 x 23 + 28 x 77 =
giúp mik zới mn ui , mik cần gấp lắm , làm ơn giúp mình ik mà mn , năn nỉ mn đó , giải tích cả cahs làm cho mik nhé , thank you mn nhìu ạ , kết quả gợi ý là 2800 mik mong các bạn sẽ trả lời đúng kết quả mà mik gợi ý , mong mn sẽ giúp mik , cảm ơn mn nhìu ạ
=23 x (58-30) + 28 x 77
=23 x 28 +28 x 77
=28 x (23+77)
=28 x 100
=2800
học tốt bạn nhé
bài này là dạng nâng cao về toán tính nhanh, mik nghĩ là ẽ ít bạn trả lời đc
Xem thêm câu trả lời
Nhờ mn giúp em vs ạ. Cảm ơn nhìu.
Bài 3:
b: Gọi K là giao điểm của AB và OP
Xét (O) có
PA,PB là các tiếp tuyến
Do đó: PA=PB
=>P nằm trên đường trung trực của BA(1)
Ta có: OA=OB
=>O nằm trên đường trung trực của BA(2)
Từ (1) và (2) suy ra PO là đường trung trực của AB
=>PO\(\perp\)AB tại K và K là trung điểm của AB
Ta có: ΔOAP vuông tại A
=>\(AP^2+AO^2=OP^2\)
=>\(AP^2=OP^2-OA^2=d^2-R^2\)
=>\(AP=\sqrt{d^2-R^2}\)
Xét ΔOAP vuông tại A có AK là đường cao
nên \(AK\cdot OP=AO\cdot AP\)
=>\(AK\cdot d=R\cdot\sqrt{d^2-R^2}\)
=>\(AK=\dfrac{R\cdot\sqrt{d^2-R^2}}{d}\)
K là trung điểm của AB
=>\(AB=2\cdot AK=\dfrac{2\cdot R\cdot\sqrt{d^2-R^2}}{d}\)
Xét (O) có
ΔBAC nội tiếp
BC là đường kính
Do đó: ΔBAC vuông tại A
=>\(BA^2+AC^2=BC^2\)
=>\(AC^2=\left(2R\right)^2-\left(\dfrac{2R\sqrt{d^2-R^2}}{d}\right)^2\)
=>\(AC^2=4R^2-\dfrac{4R^2\cdot\left(d^2-R^2\right)}{d^2}\)
=>\(AC^2=\dfrac{4R^2d^2-4R^2\left(d^2-R^2\right)}{d^2}=\dfrac{4R^4}{d^2}\)
=>\(AC=\dfrac{2R^2}{d}\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AC\cdot AB\)
=>\(AH\cdot2R=\dfrac{2R^2}{d}\cdot\dfrac{2R\sqrt{d^2-R^2}}{d}\)
=>\(AH=\dfrac{R\cdot2R\sqrt{d^2-R^2}}{d^2}=\dfrac{2R^2\cdot\sqrt{d^2-R^2}}{d^2}\)
Đúng 2
Bình luận (0)
Mn ơi giúp mik với, please please lm ơn giúp mik nka, huhu giúp mik đuy, mik cảm ơn mn rất rất nhìu nhìu lunnnnnnn. Giúp mình nha! Thank kiuuu mn

Nhờ mn giúp em vs ạ. Em cảm ơn nhìu
a: Xét (O) có
ΔABN nội tiếp
AB là đường kính
Do đó: ΔABN vuông tại N
=>AN\(\perp\)NB tại N
=>BN\(\perp\)AM tại N
Xét (O) có
ΔAHB nội tiếp
AB là đường kính
Do đó: ΔAHB vuông tại H
=>AH\(\perp\)HB tại H
=>BH\(\perp\)AD tại H
Xét ΔBAM vuông tại B có BN là đường cao
nên \(AN\cdot AM=AB^2\left(1\right)\)
Xét ΔABD vuông tại B có BH là đường cao
nên \(AH\cdot AD=AB^2\left(2\right)\)
Từ (1) và (2) suy ra \(AN\cdot AM=AH\cdot AD\)
c: ta có: ΔOAN cân tại O
mà OI là đường trung tuyến
nên OI\(\perp\)AN
Xét ΔIAO vuông tại I và ΔNBM vuông tại N có
\(\widehat{IAO}=\widehat{NBM}\left(=90^0-\widehat{AMB}\right)\)
Do đó: ΔIAO~ΔNBM
Xét tứ giác OIMB có
\(\widehat{OBM}+\widehat{OIM}=90^0+90^0=180^0\)
nên OIMB là tứ giác nội tiếp
=>\(\widehat{MOB}=\widehat{MIB}\)
Xét ΔOBM vuông tại B và ΔINB vuông tại N có
\(\widehat{BOM}=\widehat{NIB}\left(cmt\right)\)
Do đó: ΔOBM~ΔINB
Đúng 1
Bình luận (0)



























