a: Xét tứ giác AMDN có góc AMD=góc AND=góc MAN=90 độ

nên AMDN là hình chữ nhật

b: Xét tứ giác NKIM có

D là trung điểm của NI

D là trung điểm của KM

Do đó: NKIM là hình bình hành

mà NI vuông góc với KM

nên NKIM là hình thoi

c: Xét ΔABC có DN//AB

nên DN/AB=CN/CA=CD/CB

=>CN=1/2CA
hay N là trung điểm của AC

Xét ΔABC có DM//AC
nên BM/BA=BD/BC=1/2

hay BM=1/2BA
=>M là trung điểm của AB

Ta có: ΔAHB vuông tại H 

mà HM là đường trung tuyến

nên MA=MH

Ta có: ΔAHC vuông tại H

mà HN là đừog trung tuyến

nên HN=AN

Xét ΔMAN và ΔMHN có

MA=MH

AN=HN

MN chung

Do đó: ΔMAN=ΔMHN

Suy ra:góc MHN=90 độ

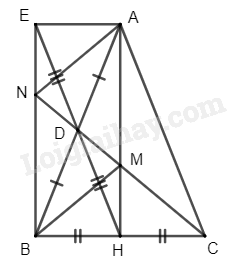
a) Vì \(\Delta ABC\) cân tại \(A\) nên \(\widehat {{\rm{ABC}}} = \widehat {{\rm{ACB}}}\) và \(AB = AC\)

Vì \(\Delta ABC\) cân tại \(A\), có \(AH\) là trung tuyến (gt)

Suy ra \(AH\) là đường cao

Suy ra \(AH \bot BC\)

Suy ra \(\widehat {{\rm{AHB}}} = \widehat {{\rm{AHC}}} = 90^\circ \)

Xét \(\Delta AHB\) vuông tại \(H\) ta có: \(HD\) là trung tuyến

Suy ra \(HD = \frac{1}{2}AB\)

Mà \(DA = DB = \frac{1}{2}AB\) (do \(D\) là trung điểm \(AB\))

Suy ra \(DA = DB = HD\)

Suy ra \(\Delta DHB\) cân tại \(D\)

Suy ra \(\widehat {{\rm{ABC}}} = \widehat {{\rm{DHB}}}\)

Mà \(\widehat {{\rm{ABC}}} = \widehat {{\rm{ACB}}}\) (cmt)

Suy ra \(\widehat {{\rm{DHB}}} = \widehat {{\rm{ACB}}}\)

Mà hai góc ở vị trí đồng vị

Suy ra \(DH\) // \(AC\)

Suy ra \(ADHC\) là hình thang

b) Vì \(E\) đối xứng với \(H\) qua \(D\) (gt)

Suy ra \(D\) là trung điểm của \(HE\)

Xét tứ giác \(AHBE\) ta có:

Hai đường chéo \(HE\) và \(AB\) cắt nhau tại trung điểm \(D\)

Suy ra \(AHBE\) là hình bình hành

Mà \(\widehat {{\rm{AHB}}} = 90^\circ \) (cmt)

Suy ra \(AHBE\) là hình chữ nhật

c) Vì \(AHBE\) là hình chữ nhật (cmt)

Suy ra \(AH\) // \(BE\) và \(AH = BE\)

Xét \(\Delta DEN\) và \(\Delta DHM\) ta có:

\(\widehat {{\rm{NED}}} = \widehat {{\rm{DHM}}}\) (do \(BE\) // \(AH\))

\(DE = DH\) (do \(D\) là trung điểm của \(HE\))

\(\widehat {{\rm{EDN}}} = \widehat {{\rm{MDH}}}\) (đối đỉnh)

Suy ra \(\Delta DEN = \Delta DHM\) (g-c-g)

Suy ra \(EN = MH\) (hai cạnh tương ứng)

Mà \(BE = AH\) (cmt)

Suy ra \(BE - EN = AH - MH\)

Suy ra \(NB = AM\)

Mà \(NB\) // \(AM\) (do \(EB\) // \(AH\))

Suy ra \(AMBN\) là hình bình hành

a)ta có : A=E=F=90 => AEHF hình chữ nhật

b)ta có: Am=AN, HM=MC =>ACNH hbh

Ta có AH//CN => AHE =CNH (đv) = FEH mà FC//NE => EFCN hìn thang cân 

c)ta có OC, AM là trung tuyến của ∆ACH cắt nhau tại G => G là trọng tâm => AG =2/3 AM=2/3*AN/2=AN/3

=>AN=3AG

a) Xét tứ giác ADHE có:

\(\left\{{}\begin{matrix}\widehat{A}=90^o\\\widehat{HDA}=90^o\\\widehat{HEA}=90^o\end{matrix}\right.\)

=> ADHE là h.c.n

b) Ta có:

\(\left\{{}\begin{matrix}\widehat{BID}=2\widehat{IHD}\\\widehat{IKE}=2\widehat{KCE}\end{matrix}\right.\)

mà \(\widehat{IHD}=\widehat{KCE}\)

=> \(\widehat{BID}=\widehat{IKE}\) mà 2 góc có vị trí đồng vị

=> DI//EK

=> DEKI là hình thang

a: XétΔAHB vuông tại H có HD là đường cao

nên \(AD\cdot AB=AH^2\left(1\right)\)

Xét ΔAHC vuông tại H có HE là đường cao

nên \(AE\cdot AC=AH^2\left(2\right)\)

Từ (1) và (2) suy ra \(AD\cdot AB=AE\cdot AC\)

a: Xét ΔABC có

H là trung điểm của BC

D là trung điểm của AB

Do đó: HD là đường trung bình

=>HD//AC

hay ADHC là hình thang

b: Xét tứ giác AHBE có

D là trung điểm chung của AB và HE

góc AHB=90 độ

Do đó: AHBE là hình chữ nhật

c: Xét ΔABH có

D là trung điểm của AB

DI//BH

Do đó; I là trung điểm của AH

Xét tứ giác AEHC có

AE//HC

AE=HC

Do đó: AEHC là hình bình hành

=>AH cắt EC tại trung điểm của mỗi đường

=>E,I,C thẳng hàng