Cho hình vuông ABCD có cạnh bằng 2a. Tính:
| AB→ - 3BC→|
Những câu hỏi liên quan
cho hình chóp s abcd có đáy abcd là hình vuông cạnh bằng 2a. Hình chiếu vuông góc của đỉnh s lên ab là điểm m nằm trong cạnh ab sao cho ma = 2mb. biết cạnh sc = 2a và góc giữa mặt phẳng (scd) và đáy (abcd) bằng 60°. Vậy khối chóp s abcd bằng?
SGK Chân trời sáng tạo
20 tháng 8 2023 lúc 20:55
Cho hình chóp \(S.ABCD\) có đáy là hình vuông cạnh bằng \(a\sqrt 2 \), có các cạnh bên đều bằng \(2a\).
a) Tính góc giữa \(SC\) và \(AB\).
b) Tính diện tích hình chiếu vuông góc của tam giác \(SAB\) trên mặt phẳng \(\left( {ABCD} \right)\).
tham khảo:
a) AB//CD nên góc giữa SC và AB là góc giữa SC và CD: \(\widehat{SCD}\)
cos\(\widehat{SCD}\)=\(\dfrac{\left(2a\right)^2+a^2-\left(2a\right)^2}{2.2a.a}=\dfrac{1}{4}\)
Suy ra \(\widehat{SCD}=75^0\)
b) Kẻ SO⊥(ABCD). Do các cạnh bên của hình chóp bằng nhau nên O là tâm của hình vuông ABCD.
Ta có: AO⊥OB;AC=\(\sqrt{2}.\sqrt{2}\).a=2a;AO=BO=\(\dfrac{1}{2}\).2a=a
Hình chiếu vuông góc của tam giác SAB là tam giác OAB có diện tích là \(\dfrac{1}{2}\).a.a=\(\dfrac{1}{2}.a^2\)
Đúng 1
Bình luận (0)
Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2a, tam giác SAB đều, góc giữa (SCD) và (ABCD) bằng
60
0
. Gọi M là trung điểm của cạnh AB. Biết hình chiếu vuông góc của đỉnh S trên mặt phẳng (ABCD) nằm trong hình vuông ABCD. Tính theo a khoảng cách giữa hai đường thẳng SM và AC.
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2a, tam giác SAB đều, góc giữa (SCD) và (ABCD) bằng 60 0 . Gọi M là trung điểm của cạnh AB. Biết hình chiếu vuông góc của đỉnh S trên mặt phẳng (ABCD) nằm trong hình vuông ABCD. Tính theo a khoảng cách giữa hai đường thẳng SM và AC.
Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2a, tam giác SAB đều, góc giữa (SCD) và (ABCD) bằng
60
°
. Gọi M là trung điểm của cạnh AB. Biết hình chiếu vuông góc của đỉnh S trên mặt phẳng (ABCD) nằm trong hình vuông ABCD. Tính theo a khoảng cách giữa hai đường thẳng SM và AC A.
a
5
5
B.
5
a
3...
Đọc tiếp
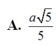
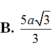
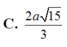
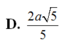
Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2a, tam giác SAB đều, góc giữa (SCD) và (ABCD) bằng 60 ° . Gọi M là trung điểm của cạnh AB. Biết hình chiếu vuông góc của đỉnh S trên mặt phẳng (ABCD) nằm trong hình vuông ABCD. Tính theo a khoảng cách giữa hai đường thẳng SM và AC
A. a 5 5
B. 5 a 3 3
C. 2 a 15 3
D. 2 a 5 5
Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2a, tam giác SAB đều, góc giữa (SCD) và (ABCD) bằng
60
0
. Gọi M là trung điểm của cạnh AB. Biết hình chiếu vuông góc của đỉnh S trên mặt phẳng (ABCD) nằm trong hình vuông ABCD. Tính theo a khoảng cách giữa hai đường thẳng SM và AC A.
a
5
5
B.
5
a...
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2a, tam giác SAB đều, góc giữa (SCD) và (ABCD) bằng 60 0 . Gọi M là trung điểm của cạnh AB. Biết hình chiếu vuông góc của đỉnh S trên mặt phẳng (ABCD) nằm trong hình vuông ABCD. Tính theo a khoảng cách giữa hai đường thẳng SM và AC
A. a 5 5
B. 5 a 3 3
C. 2 a 15 3
2 a 5 5
Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2a, tam giác SAB đều, góc giữa (SCD) và (ABCD) bằng
60
°
. Gọi M là trung điểm của cạnh AB. Biết hình chiếu vuông góc của đỉnh S trên mặt phẳng (ABCD)nằm trong hình vuông ABCD. Tính theo a khoảng cách giữa hai đường thẳng SM và AC A.
a
5
5
B.
5
a
3...
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2a, tam giác SAB đều, góc giữa (SCD) và (ABCD) bằng 60 ° . Gọi M là trung điểm của cạnh AB. Biết hình chiếu vuông góc của đỉnh S trên mặt phẳng (ABCD)nằm trong hình vuông ABCD. Tính theo a khoảng cách giữa hai đường thẳng SM và AC
A. a 5 5
B. 5 a 3 3
C. 2 a 15 5
D. 2 a 5 5
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật có cạnh AB a, BC 2a. Cạnh SA vuông góc với mặt phẳng đáy (ABCD), SA 2a. Khoảng cách giữa hai đường thẳng BD và SC bằng A.
a
2
3
B.
a
3
2
C.
3
a...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật có cạnh AB = a, BC = 2a. Cạnh SA vuông góc với mặt phẳng đáy (ABCD), SA = 2a. Khoảng cách giữa hai đường thẳng BD và SC bằng
A. a 2 3
B. a 3 2
C. 3 a 2
D. 2 a 3
Đáp án D
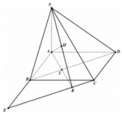
Dựng 
Dựng 
Khi đó Cx cắt AB tại E và AK tại I suy ra BI là đường trung bình của ∆AEK ( Do BD qua trung điểm O của AC)
Ta có: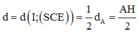 
Do 
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật có cạnh ABa, BC2a. Cạnh SA vuông góc với mặt phẳng đáy (ABCD), SA2a. Khoảng cách giữa hai đường thẳng BD và SC bằng
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật có cạnh AB=a, BC=2a. Cạnh SA vuông góc với mặt phẳng đáy (ABCD), SA=2a. Khoảng cách giữa hai đường thẳng BD và SC bằng
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, cạnh bằng 4a. Cạnh bên SA2a. Hình chiếu vuông góc của đỉnh S trên mặt phẳng (ABCD)là trung điểm của H của đoạn thẳng AO. Tính khoảng cách d giữa các đường thẳng SD và AB A.d4a B.
d
4
a
22
11
C.d2a D.
d...
Đọc tiếp
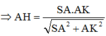
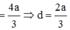
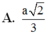
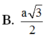
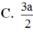
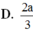
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, cạnh bằng 4a. Cạnh bên SA=2a. Hình chiếu vuông góc của đỉnh S trên mặt phẳng (ABCD)là trung điểm của H của đoạn thẳng AO. Tính khoảng cách d giữa các đường thẳng SD và AB
A.d=4a
B. d = 4 a 22 11
C.d=2a
D. d = 3 a 2 11
Cho hình chóp S.ACBD có đáy ABCD là hình thang đáy AB và CD với A B = 2 C D = 2 a , cạnh bên SA vuông góc với mặt phẳng đáy và S A = a 3 . Tính chiều cao h của hình thang ABCD biết khối chóp S.ABCD có thể tích bằng
A. h = 2a
B. h = 4a
C. h = 6a
D. h = a
