hình chóp đều có các mặt bên là tam giác đều thì đáy có hình gì,cho hai trường hợp nhé

Những câu hỏi liên quan
Quan sát hình 120 và điền cụm từ và số thích hợp vào các ô trống ở bảng sau, biết rằng các hình đã cho là những hình chóp đều.
Chóp tam giác đều
Chóp tứ giác đều
Chóp ngũ giác đều
Chóp lục giác đều
Đáy
Tam giác đều
Mặt bên
Tam giác cân
Số cạnh đáy
5
Số cạnh
10
Số mặt
5
Đọc tiếp
Quan sát hình 120 và điền cụm từ và số thích hợp vào các ô trống ở bảng sau, biết rằng các hình đã cho là những hình chóp đều.
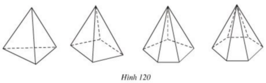
| Chóp tam giác đều | Chóp tứ giác đều | Chóp ngũ giác đều | Chóp lục giác đều | |
| Đáy | Tam giác đều | |||
| Mặt bên | Tam giác cân | |||
| Số cạnh đáy | 5 | |||
| Số cạnh | 10 | |||
| Số mặt | 5 |
| Chóp tam giác đều | Chóp tứ giác đều | Chóp ngũ giác đều | Chóp lục giác đều | |
| Đáy | Tam giác đều | Hình vuông | Ngũ giác đều | Lục giác đều |
| Mặt bên | Tam giác cân | Tam giác cân | Tam giác cân | Tam giác cân |
| Số cạnh đáy | 3 | 4 | 5 | 6 |
| Số cạnh | 6 | 8 | 10 | 12 |
| Số mặt | 4 | 5 | 6 | 7 |
Đúng 0
Bình luận (0)
Nếu đặt mặt đáy của hình chóp đều đáy hình vuông song song với mặt phẳng chiếu bằng thì hình chiếu bằng là hình gì?
A. Hình vuông.
B. Hình vuông có hai đường chéo.
C. Hình tam giác cân.
D. Hình tam giác đều.
Nếu đặt mặt đáy của hình chóp đều đáy hình vuông song song với mặt phẳng chiếu bằng thì hình chiếu bằng là hình gì?
A. Hình vuông.
B. Hình vuông có hai đường chéo.
C. Hình tam giác cân.
D. Hình tam giác đều.
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Hình chóp tứ giác đều S.ABCD có đáy là hình vuông cạnh a, các mặt bên của mình chóp là các tam giác đều. Tính đường cao SH của hình chóp đó. A. SH
a
3
2
B. SH
a
2
C. SH
a
2
2
D. SH
a
2
3
Đọc tiếp
Hình chóp tứ giác đều S.ABCD có đáy là hình vuông cạnh a, các mặt bên của mình chóp là các tam giác đều. Tính đường cao SH của hình chóp đó.
A. SH = a 3 2
B. SH = a 2
C. SH = a 2 2
D. SH = a 2 3
Cho hình chóp S.ABC có đáy ABC là tam giác đều có cạnh là a. Mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc vơi đáy. Tính thể tích của khối cầu ngoại tiếp hình chóp.
A
.
15
πa
3
9
B
.
5
15
πa
3...
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác đều có cạnh là a. Mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc vơi đáy. Tính thể tích của khối cầu ngoại tiếp hình chóp.
A . 15 πa 3 9
B . 5 15 πa 3 54
C . 5 15 πa 3 18
D . 4 3 πa 3 27
Đáp án B.
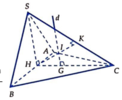
Gọi H là trung điểm AB, G là trọng tâm tam giác ABC, K là trung điểm SC.
Ta có: ![]()
SH = SC => HK là trung trực SC. Qua O kẻ trục d//SH => d ⊥ (ABC)
Gọi
![]()
=> I là tâm mặt cầu ngoại tiếp hình chóp SABC
Ta có
![]()
Xét ∆ HIG vuông tại G:
![]()
Vậy thể tích khối cầu ngoại tiếp hình chóp
![]()
Đúng 0
Bình luận (0)
Cho S.ABC là hình chóp tam giác đều có các cạnh bên bằng a và có góc giữa các mặt bên và mặt phẳng đáy là α. Hình nón đỉnh S có đường tròn đáy nội tiếp tam giác đều ABC gọi là hình nón nội tiếp hình nón đã cho. Hãy tính diện tích xung quanh của hình nón này theo a và α
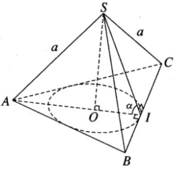
Gọi I là trung điểm của cạnh BC và O là tâm của tam giác đều ABC. Theo giả thiết ta có SA = SB = SC = a và ∠ SIO = α. Đặt OI = r, SO = h, ta có AO = 2r và

Do đó a 2 = r 2 tan 2 α + 4 r 2 = r 2 tan 2 α + 4
Vậy 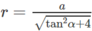
Hình nón nội tiếp có đường sinh là :
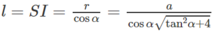
Diện tích xung quanh của hình nón nội tiếp hình chóp S.ABC là:
![]()
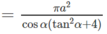
Đúng 0
Bình luận (0)
Trong các phát biểu sau, phát biểu nào đúng?a) Hình chóp đều S.ABCD có đáy là hình bình hành.b) Hình chóp đều S.ABCD có đáy là hình thoi, chân đường cao hình chóp là giao điểm của 2 đường chéo hình thoi.c) Hình chóp đều S.ABCD có đáy là hình vuông, chân đường cao hình chóp là giao điểm của 2 đường chéo hình vuông.d) Hình chóp đều S.ABCD có đáy là hình vuông, các mặt bên là các tam giác đều chung đỉnh S.
Đọc tiếp
Trong các phát biểu sau, phát biểu nào đúng?
a) Hình chóp đều S.ABCD có đáy là hình bình hành.
b) Hình chóp đều S.ABCD có đáy là hình thoi, chân đường cao hình chóp là giao điểm của 2 đường chéo hình thoi.
c) Hình chóp đều S.ABCD có đáy là hình vuông, chân đường cao hình chóp là giao điểm của 2 đường chéo hình vuông.
d) Hình chóp đều S.ABCD có đáy là hình vuông, các mặt bên là các tam giác đều chung đỉnh S.
Cho hình chóp đều S.ABCD có đáy ABCD là hình vuông cạnh bằng 4cm, các mặt bên là tam giác cân có độ dài cạnh bên là 6cm. Diện tích xung quanh của hình chóp đã cho là? A.
32
c
m
2
B.
32
2
c
m
2
C.
16
2
c
m
2
D.
16
c
m
2...
Đọc tiếp
Cho hình chóp đều S.ABCD có đáy ABCD là hình vuông cạnh bằng 4cm, các mặt bên là tam giác cân có độ dài cạnh bên là 6cm. Diện tích xung quanh của hình chóp đã cho là?
A. 32 c m 2
B. 32 2 c m 2
C. 16 2 c m 2
D. 16 c m 2
Cho hình chóp đều S.ABCD có đáy ABCD là hình vuông cạnh bằng 4cm, các mặt bên là tam giác cân có độ dài cạnh bên là 6cm. Diện tích xung quanh của hình chóp đã cho là? A.
32
(
c
m
2
)
B.
32
2
(
c
m
2
)
C.
16
(
c
m
2
)
D. ...
Đọc tiếp
Cho hình chóp đều S.ABCD có đáy ABCD là hình vuông cạnh bằng 4cm, các mặt bên là tam giác cân có độ dài cạnh bên là 6cm. Diện tích xung quanh của hình chóp đã cho là?
A. 32 ( c m 2 )
B. 32 2 ( c m 2 )
C. 16 ( c m 2 )
D. 16 ( c m 2 )
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. Mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích V khối cầu ngoại tiếp hình chóp S.ABC A.
V
4
3
π
a
3
27
B.
V
5
15...
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. Mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích V khối cầu ngoại tiếp hình chóp S.ABC
A. V = 4 3 π a 3 27
B. V = 5 15 π a 3 54
C. V = 5 15 π a 3 18
D. V = 5 π a 3 3
Đáp án B
Ta có: O là giao điểm của trục đường tròn ngoại tiếp tam giác ABC và SAB.
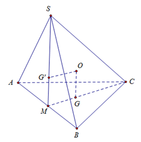
Ta có: O G = 1 3 S M = 3 6 ; M G = C M 3 = 3 6
R = S O = M G 2 + S G 2 = 3 6 + 1 3 = 15 6
Cách 2: Áp dụng CT giải nhanh trong trường hợp S A B ⊥ A B C ta có:
R 2 = R 2 A B C + R 2 S A B − A B 2 4 = 1 2 3 + 1 2 3 − 1 4 = 2 3 − 1 4 = 5 12 ⇒ R = 15 6 .
Vậy V = 4 3 π R 3 = 5 15 π 54 .
Đúng 0
Bình luận (0)
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. Mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Thể tích của khối chóp S.ABC là: A.
a
3
6
B.
a
3
3
C.
a
3
8
D.
2
a
3
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. Mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Thể tích của khối chóp S.ABC là:
A. a 3 6
B. a 3 3
C. a 3 8
D. 2 a 3
Đáp án C
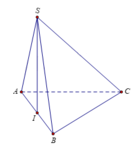
Gọi I là trung điểm của A B ⇒ S I ⊥ A B C
Ta có S I = a 2 − a 2 2 = a 3 2 ; S A B C = 1 2 a 2 sin 60 ° = a 2 3 4
Thể tích của khối chóp S . A B C là:
V = 1 3 S I . S A B C = 1 3 . a 3 2 . a 2 3 4 = a 3 8
Đúng 0
Bình luận (0)












