22100+32100=R. Tìm số tận cung của R.

Những câu hỏi liên quan
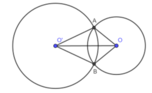
Cho hai đường tròn (O; R) và (O': R) cắt nhau tại A, B. Hãy so sánh R và R' trong các trường hợp sau :
a) Số đo cung nhỏ AB của (O;R) lớn hơn số đo cung nhỏ AB của (O'; R')
b) Số đo cung lớn AB của (O;R) nhỏ hơn số đo cung lớn AB của (O'; R')
c) Số đo hai cung nhỏ bằng nhau.
cho a và b là các số tự nhiên lớn hơn 1. cmr: chữ số tận cùng của a^4k + r sẽ trùng với chữ số tận cùng của a^r. với r bất kì
Cho hai đường tròn (O; R) và (O’ ; R’) cắt nhau tại A ,B .Hãy so sánh R và R’ trong các trường hợp sau: Số đo cung nhỏ AB của (O ;R) nhỏ hơn số đo cung nhỏ AB của (O’ ;R’)
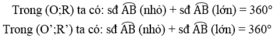
Vì số đo cung lớn AB của (O;R) nhỏ hơn số đo cung lớn AB của (O’;R’) nên số đo cung nhỏ AB của (O;R) lớn hơn số đo cung nhỏ AB của (O’;R’)
Như vậy, trường hợp này tương tự như giả thiết trong câu a.Chứng minh tương tự ta được R’ > R
Đúng 0
Bình luận (0)
Cho hai đường tròn (O; R) và (O’ ; R’) cắt nhau tại A ,B .Hãy so sánh R và R’ trong các trường hợp sau: Số đo cung nhỏ AB của (O ;R) lớn hơn số đo cung nhỏ AB của (O’ ;R’)
Cho AB=r căn 3 là dây cung của đường tròn (O,r) số đo cung lớn AB?
Kẻ OH⊥AB tại H
Xét ΔOAB có OA=OB(=R)
nên ΔOAB cân tại O(Định nghĩa tam giác cân)
Ta có: ΔOAB cân tại O(cmt)
mà OH là đường cao ứng với cạnh đáy AB(gt)
nên OH là đường trung tuyến và cũng là đường phân giác ứng với cạnh AB(Định lí tam giác cân)
hay H là trung điểm của AB
\(\Leftrightarrow AH=\dfrac{AB}{2}=\dfrac{R\sqrt{3}}{2}\)
Xét ΔOAH vuông tại H có
\(\sin\widehat{AOH}=\dfrac{AH}{AO}=\dfrac{R\cdot\dfrac{\sqrt{3}}{2}}{R}=\dfrac{\sqrt{3}}{2}\)
hay \(\widehat{AOH}=60^0\)
\(\Leftrightarrow\widehat{AOB}=2\cdot\widehat{AOH}=120^0\)
Số đo cung lớn AB là: \(360^0-120^0=240^0\)
Đúng 1
Bình luận (0)
Cho (O;R) và một dây cung AB = R căn 3 số đo của cung nhỏ AB là
Tham khảo:
Kẻ OH⊥AB tại H
Xét ΔOAB có OA=OB(=R)
nên ΔOAB cân tại O(Định nghĩa tam giác cân)
Ta có: ΔOAB cân tại O(cmt)
mà OH là đường cao ứng với cạnh đáy AB(gt)
nên OH là đường trung tuyến và cũng là đường phân giác ứng với cạnh AB(Định lí tam giác cân)
hay H là trung điểm của AB
⇔AH=AB/2=R√3/2
Xét ΔOAH vuông tại H có
sinˆAOH=AH/AO=R⋅√3/2/R=√3/2
hay ˆAOH=60 độ
⇔ˆAOB=2⋅ˆAOH=120 độ (số đo cung nhỏ nhé)
Số đo cung lớn AB là: 360−120=240 độ
Chúc em học tốt
Đúng 1
Bình luận (0)
1. Cho tam giác ABC có A 60o nội tiếp trong đường tròn (O;R)a) tính số đo cung BCb) tính độ dài dây cung BC và độ dài cung BC theo Rc) tính diện tích hình quạt ứng với góc ở tâm BOC theo R2. CHo (O;R) và dây AB Rsqrt{2}a) tính số đo cung AB, số đo góc AOBb)| tính theo R độ dài cung ABtính diện tích của hình viên phân giới hạn bởi dây AB và cung nhỏ AB theo R
Đọc tiếp
1. Cho tam giác ABC có A= 60o nội tiếp trong đường tròn (O;R)
a) tính số đo cung BC
b) tính độ dài dây cung BC và độ dài cung BC theo R
c) tính diện tích hình quạt ứng với góc ở tâm BOC theo R
2. CHo (O;R) và dây AB= R\(\sqrt{2}\)
a) tính số đo cung AB, số đo góc AOB
b)| tính theo R độ dài cung AB
tính diện tích của hình viên phân giới hạn bởi dây AB và cung nhỏ AB theo R
Cho đường tròn tâm O bán kính R và dây AB = R√3. Tính số đo của 2 cung AB( Cung nhỏ và lớn)
Cho đường tròn (O, r) đường kính Bc. Lấy dây AD = R, dây AC và BD cắt nhau tại E. Tìm số đo cung nhỏ AC
Chưa đủ dữ kiện để tính sđc AC nhỏ bạn nhé. Bạn xem lại đề.
Đúng 0
Bình luận (0)