Cho A= x3+y3+x3-3xyz
a) CMR nếu x+y+z=0 thì A=0
b) Điều ngược lại có đúng không
cho A= x^3+y^3+z^3-3xyz.
1. CMR: nếu x+y+z=0 thì A=0
2. Điều ngược lại có đúng ko?
Cần Gấp!!!!!
THANKS!
1;\(A=x^3+y^3+z^3-3xyz\)
\(A=\left(x+y\right)^3-3xy\left(x+y\right)+z^3-3xyz\)
\(A=\left(x+y+z\right)\left[\left(x+y\right)^2-\left(x+y\right)z+z^2\right]-3xy\left(x+y+z\right)\)
\(A=\left(x+y+z\right)\left(x^2+y^2+z^2-xy-yz-xz\right)=0\)
2;Nếu A = 0
Điều ngược lại đúng khi x^2+y^2+z^2-xy-yz-xz khác 0
Ta đi chứng minh A phụ thuộc vào x+y+z
\(A=x^3+y^3+z^3-3xyz.\)
\(=\left(x+y\right)^3-3xy\left(x+y\right)+z^3-3xyz\)
\(=\left(x+y+z\right)\left[\left(x+y\right)^2-z\left(x+y\right)+z^2\right]-3xy\left(x+y+z\right)\)
\(=\left(x+y+z\right)\left(x^2+2xy+y^2-xz-yz+z^2-3xy\right)\)
\(=\left(x+y+z\right)\left(x^2+y^2+z^2-xy-yz-xz\right)\)
Mà x^2+y^2+z^2-xy-yz-xz>0
nên x+y+z =0 thì A=0
Cho các số thực x, y , z thỏa mãn 2 điều kiện :
a) (x + y) ( y + z)( z + x) = xyz
b) (x3 + y3 ) (y3 + z3) ( x3 + z3) = x3y3z3
CMR: xyz =0
a) Chứng minh nếu x + y + z = 0 thì x 3 + y 3 + z 3 = 3xyz.
b) Áp dụng. Phân tích các đa thức sau thành nhân tử:
P = ( a 2 + b 2 ) 3 + ( c 2 - a 2 ) 3 - ( b 2 + c 2 ) 3 .
CMR
a) xyz≠0, 1/x+1/y+1/z=0 thì (x2y2+y2z2+z2x2)2=2(x4y4+y4z4+z4x4)
b) x+y+z=0 thì x3+y3+z3-3xyz=0
cho A=x^3+y^3+z^3=3xyz. CM nếu x=y=z=0 thì A=0 và điều ngược lại
cho x+y+z=2 và x3+y3+z3-3xyz=0. CMR:x=y=z
\(x^3+y^3+z^3-3xyz=0\)
\(\Leftrightarrow\left(x+y\right)^3+z^3-3xy\left(x+y\right)-3xyz=0\)
\(\Leftrightarrow\left(x+y+z\right)\left(x^2+2xy+y^2-xz-yz+z^2-3xy\right)=0\)
\(\Leftrightarrow x^2+y^2+z^2-xy-xz-yz=0\)
\(\Leftrightarrow x=y=z\)
Chứng minh: x 3 + y 3 + z 3 - 3 x y z = 1 / 2 . x + y + z x - y 2 + y - z 2 + z - x 2
Từ đó chứng tỏ: Với ba số a, b, c không âm thì x 3 + y 3 + z 3 3 ≥ x y z
(Bất đẳng thức Cô-si cho ba số không âm)
Dấu đẳng thức xảy ra khi ba số a, b, c bằng nhau.
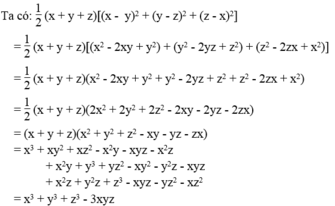
Vế trái bằng vế phải nên đẳng thức được chứng minh.
Nếu a ≥ 0, b ≥ 0, c ≥ 0 thì :
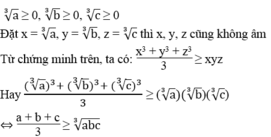
Cho \(A=x^3+y^3+z^3-3xyz\)
a) CMR: Nếu x+y+z=0 thì A=0
b) Điều ngược lại có đúng không?
Chứng minh: x 3 + y 3 + z 3 - 3 x y z = 1 / 2 . x + y + z x - y 2 + y - z 2 + z - x 2
Từ đó chứng tỏ: Với ba số x, y, z không âm thì x 3 + y 3 + z 3 3 ≥ x y z
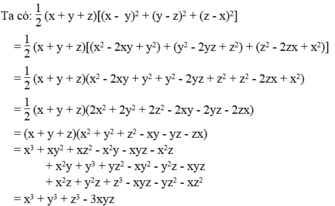
Vế trái bằng vế phải nên đẳng thức được chứng minh.
Nếu x ≥ 0, y ≥ 0, z ≥ 0 thì:
x + y + z ≥ 0
x - y 2 + y - z 2 + z - x 2 ≥ 0
Suy ra:
x 3 + y 3 + z 3 - 3 x y z ≥ 0 ⇔ x 3 + y 3 + z 3 ≥ 3 x y z
Hay: x 3 + y 3 + z 3 3 ≥ x y z