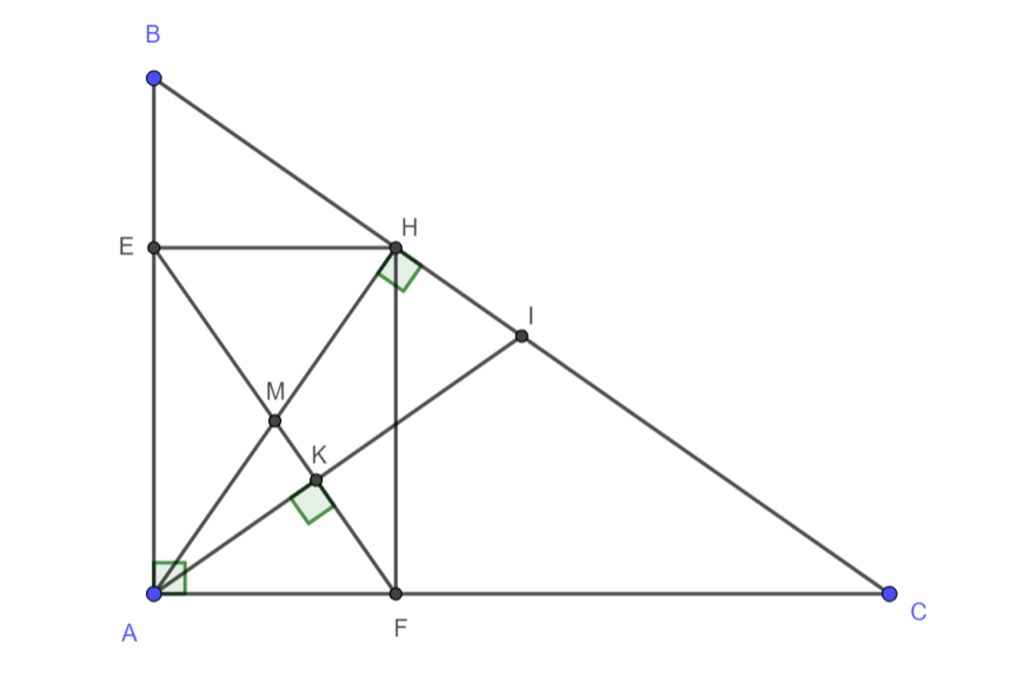
Cho tam giác ABC vuông tại B \(\left(\widehat{C}\ne30^o\right)\). Gọi E, F lần lượt là trung điểm của BC và AC. Đường phân giác của góc BAC cắt EF tại I, cắt BC tại K.
a. Tứ giác ABEF là hình gì? Tại sao?
b. Chứng minh rằng: \(\frac{AB}{BK}=\frac{EI}{EK};\frac{KC}{KE}=\frac{AC}{IE}\)
c. Qua K kẻ KH⊥AC tại H. Chứng minh rằng: ΔBKH đồng dạng với ΔAFI
d. Chứng minh: \(S_{ABC}=S_{ABIH}\)
Giúp ý d thôi ạ.