chứng minh bất đẳng thức sau ;
\(\left(1+\frac{a}{b}\right)\left(1+\frac{b}{c}\right)\left(1+\frac{c}{a}\right)\ge8\) với \(\left(\forall a,b,c>0\right)\)
các bạn giải chi tiết ra giùm mình nhé! cảm ơn nhiều à nhen !
Chứng minh các bất đẳng thức sau: a 3 b 3 = a b 3
a 3 b 3 = a 3 3 . b 3 3 = a b 3
Vế trái bằng vế phải nên đẳng thức được chứng minh.
Chứng minh các bất đẳng thức sau: a b 2 3 = 1 b a b 3 b ≠ 0
a b 2 3 = a b b 3 3 = 1 b a b 3 b ≠ 0
Vế trái bằng vế phải nên đẳng thức được chứng minh.
Chứng minh các bất đẳng thức sau ( n ∈ N ∗ ) sin 2 n α + cos 2 n α ≤ 1 .
Chứng minh các bất đẳng thức sau với x, y, z > 0
CHỨNG MINH BẤT ĐẲNG THỨC SAU
4=5
Chứng minh:4 = 5
-->Ta có
-20 = -20
<=> 25 - 45 = 16 - 36
=> 5^2 - 2.5.9/ 2 = 4^2 - 2.4.9/2
Cộg cả 2 vế với (9/2)^2 để xuất hiện hằg đẳg thức :
5^2 - 2.5.9/2 + (9/2)^2 = 4^2 - 2.4.9/2 + (9/2)^2
<=> (5 - 9/2)^2 = (4 - 9/2 )^2
=> 5 - 9/2 = 4 - 9/2
=> 5 = 4
ủa máy mk bị lỗi hay sao ấy
ko nhìn thấy bđt nào cả
chỉ thấy kêu cm 4=5![]()
Chứng minh các bất đẳng thức sau: tan x > x 0 < x < π 2
Xét hàm số y = f(x) = tanx – x trên khoảng (0; π/2)
Ta có: y’ = 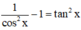 > 0 với ∀ x ∈ R.
> 0 với ∀ x ∈ R.
⇒ hàm số đồng biến trên khoảng (0; π/2)
⇒ f(x) > f(0) = 0 với ∀ x > 0
hay tan x – x > 0 với ∀ x ∈ (0; π/2)
⇔ tan x > x với ∀ x ∈ (0; π/2) (đpcm).
Chứng minh các bất đẳng thức sau: \(\dfrac{x^2+1}{x}\ge2\)
BĐT này sai nha bạn.
Nó chỉ đúng khi \(x>0\)
Với \(x>0\) thì bất đẳng thức tương đương với \(x^2+1\ge2x\)
\(\Leftrightarrow x^2-2x+1\ge0\) \(\Leftrightarrow\left(x-1\right)^2\ge0\) (luôn đúng)
\(\Rightarrow\) Điều cần chứng minh là đúng
Chứng minh các bất đẳng thức sau: tanx > sinx, 0 < x < π /2
Xét hàm số f(x) = tanx − sinx trên nửa khoảng [0; π /2);

x ∈ [0;1/2)
Dấu “=” xảy ra khi x = 0.
Suy ra f(x) đồng biến trên nửa khoảng [0; π /2)
Mặt khác, ta có f(0) = 0, nên f(x) = tanx – sinx > 0 hay tanx > sinx với mọi x ∈ [0; 1/2)
Chứng minh các bất đẳng thức sau: tan x > x + x 3 3 0 < x < π 2
Xét hàm số y = g(x) = tanx - x - 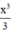 trên
trên 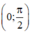
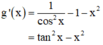
Theo kết quả câu a): tanx > x ∀ x ∈ 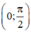
⇒ g'(x) > 0 ∀ x ∈ 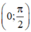
⇒ y = g'(x) đồng biến trên 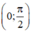
⇒ g(x) > g(0) = 0 với ∀ x ∈ 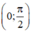
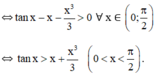
Chứng minh các bất đẳng thức sau ( n ∈ N ∗ ) 2 n + 2 > 2 n + 5
Với n = 1 thì 2 1 + 2 = 8 > 7 = 2 . 1 + 5
Giả sử bất đẳng thức đúng với n = k ≥ 1 tức là 2k + 2 > 2k + 5 (1)
Ta phải chứng minh nó cũng đúng với n = k + 1,
tức là 2k + 3 > 2(k + 1) + 5 hay 2k + 3 > 2k + 7(2)
Thật vậy, nhân hai vế của (1) với 2, ta được
2k + 3 > 4k + 10 = 2k + 7 + 2k + 3
Vì 2k + 3 > 0 nên 2k + 3 > 2k + 7(đpcm)