Cho đường tròn O bán kính r
và một dâyAB = 1,6 R, 1 tiếp tuyến // với a, bỏ cắt các tia OA, OB theo thứ tự tại M và N .Tính diện tích ∆OMN
Cho đường tròn (O; R) và dây AB = 1,6R. Vẽ một tiếp tuyến song song với AB cắt các tia
OA, OB theo thứ tự tại M và N. Tính diện tích tam giác OMN.
Cho đường tròn (O; R) và dây AB = 8 5 R. Vẽ một tiếp tuyến song song vói AB, cắt các tia OA, OB lần lượt tại M và N. Tính diện tích tam giác OMN
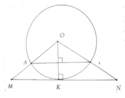
Tiếp tuyến MN, tiếp điểm K. Vì AB//MN
Nên OH ⊥ AB. Tính được OH = 3 5 R. Từ đó tính được KN = 4 3 R => S O M N = 4 3 R 2
Cho đường tròn tâm O bán kính R . Có 2 bán kính OB và OC vuông gíc với nhau . Các tiếp tuyến B và C cát nhau tại A.
1, Chứng minh tứ giác ABOC là hình vuông .
2 , Tia OA cắt đường tròn tâm O tại M . Tiếp tuyến M của đường tròn tâm O cắt AB và AC lần lượt tai D và E . Tính góc DOE
3 , Tính chu vi tam giác ADE và cạnh MB theo R
Từ một điểm A nằm ngoài đường tròn (O) bán kính R,kẻ hai tiếp tuyến AM,AN với đường tròn (M,N là các tiếp điểm)
a)Chứng minh rằng:A,M,O,N cùng thuộc một đường tròn.
b)Gọi H là giao điểm của AO và MN.Biết AO=2R.Tính AH,OH theo R.
c)Từ A kẻ cát tuyến A,B,C bất kì(B nằm giữa A và C)tiếp tuyến tại B của đường tròn (O)cắt AM,AN theo thứ tự tại P và Q.Qua điểm O kẻ đường thẳng vuông góc với OA cắt tia AM tại I và cắt tia AN tại K.Chứng minh rằng:IP+KQ\(\ge\)IK
Cho đường tròn tâm O bán kính R và một điểm M sao cho OM=2R,từ M kẻ hai tiếp tuyến MA,MB của đường tròn tâm O bán kính R (A,B là tiếp điểm).
a)Chứng minh tam giác MAB đều,tính AM theo R
b)Qua điểm C thuộc ucng nhỏ AB vẽ tiếp tuyến với đường tròn tâm O bán kính R cắt MA tại E,cắt MB tại F,OF cắt AB tại K,OE cắt AB tại H.Chứng minh EK vuống góc với OF
c)Khi số đo cung BC=90 độ.Tính EF và diện tích tam giác OHK theo R
Cho đường tròn (O; R) và BC là đường kính. Trên tia đối của tia BC lấy điểm A. Qua A vẽ hai tiếp tuyến AD, AE với đường tròn (O; R), (D, E là các tiếp điểm). Kẻ DH vuông góc với EC tại H. DE, DH cắt AC thứ tự tại I và K. a) Chứng minh bốn điểm A, D, O, E cùng thuộc một đường tròn. Xác định tâm và bán kính của đường tròn đó. b) Cho AO = 3R. Tính AE và OI theo R. c) Chứng minh rằng: 2IE2 = DK.DH. d) Qua I kẻ đường thẳng song song với EC cắt DH tại M. Kéo dài CM cắt đường tròn (O; R) tại điểm thứ hai là N. Chứng minh đường thẳng DN đi qua trung điểm của AI.
a: Xét tứ giác ODAE có
góc ODA+góc OEA=180 độ
=>ODAE là tứ giác nội tiếp
b: \(AE=\sqrt{\left(3R\right)^2-R^2}=2\sqrt{2}\cdot R\)
\(OI=\dfrac{OE^2}{OA}=\dfrac{R^2}{3R}=\dfrac{R}{3}\)
c: Xét ΔDIK vuông tại I và ΔDHE vuông tại H có
góc IDK chung
=>ΔDIK đồng dạng vơi ΔDHE
=>DI/DH=DK/DE
=>DH*DK=DI*DE=2*IE^2
1. Cho đường tròn tâm O đường kính AB, vẽ đường tròn tâm M đường kính OA. bán kính OC của đường tròn O cắt M tại D, vẽ CD vuông góc với AB. Tứ giác ADCH là hình gì?
2.Cho (O;R) Vẽ 2 bán kính OA;OB. Trên OA và OB lấy các điểm M,N sao cho OM=ON. Vẽ dây BC đi qua MN (M nằm giữa C và N)
a. So sánh MC và ND
b.Biết AOB=90 độ và CM=MN=MD. Tính OM theo R
3.Cho tam giác ABC nhọn nội tiếp đường tròn tâm O và cá góc A=45 độ. 2 đường tròn BE và CF cắt nhau tại E. CMR: B,E,O,F,C cùng nằm trên 1 đường tròn.
Bài 2 nếu ai giải được thì làm ơn gửi cho mình cách giải nhé!!Mình cũng có bài này mà ko giải được
Cho đường tròn (O;R) và một điểm A ngoài đường tròn (O) sao cho OA = 3R. Từ A vẽ hai tiếp tuyến AB, AC với (O) (B, C là các tiếp điểm). a) Chứng minh tứ giác OBAC nội tiếp và OA vuông góc với BC b) Từ B vẽ đường thẳng song song với AC cắt đường tròn tâm (O) tại D (D khác B), AD cắt đường tròn (O) tại E (E khác D). Tính tích AD.AE theo R. c) Tia BE cắt AC tại F. Chứng minh F là trung điểm AC. d) Tính theo R diện tích tam giác BDC.
bạn sáng ko đc trả lời spam
GIÚP MÌNH VỚI !!!
Cho nửa đường tròn (O; R) đường kính AB và một điểm E di động trên nửa đường tròn đó (E không trùng với A và B). Vẽ các tia tiếp tuyến Ax, By với nửa đường tròn. Tia AE cắt By tại C, tia BE cắt Ax tại D.a) Chứng minh rằng tích AD.BC không đổi. b) Tiếp tuyến tại E của nửa đường tròn cắt Ax, By theo thứ tự tại M và N. Chứng minh rằng ba đường thẳng MN, AB, CD đồng quy hoặc song song với nhau.c) Xác định vị trí của điểm E trên nửa đường tròn để diện tích tứ giác ABCD nhỏ nhất. Tính diện tích nhỏ nhất đó.