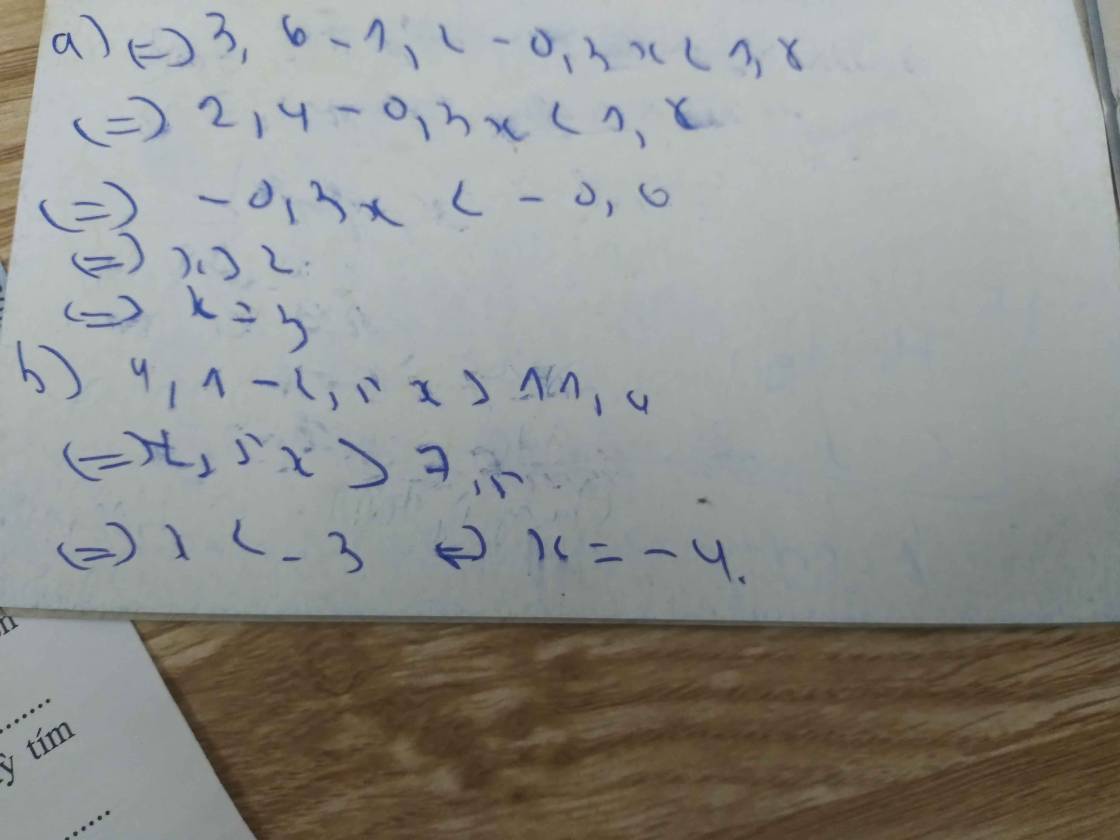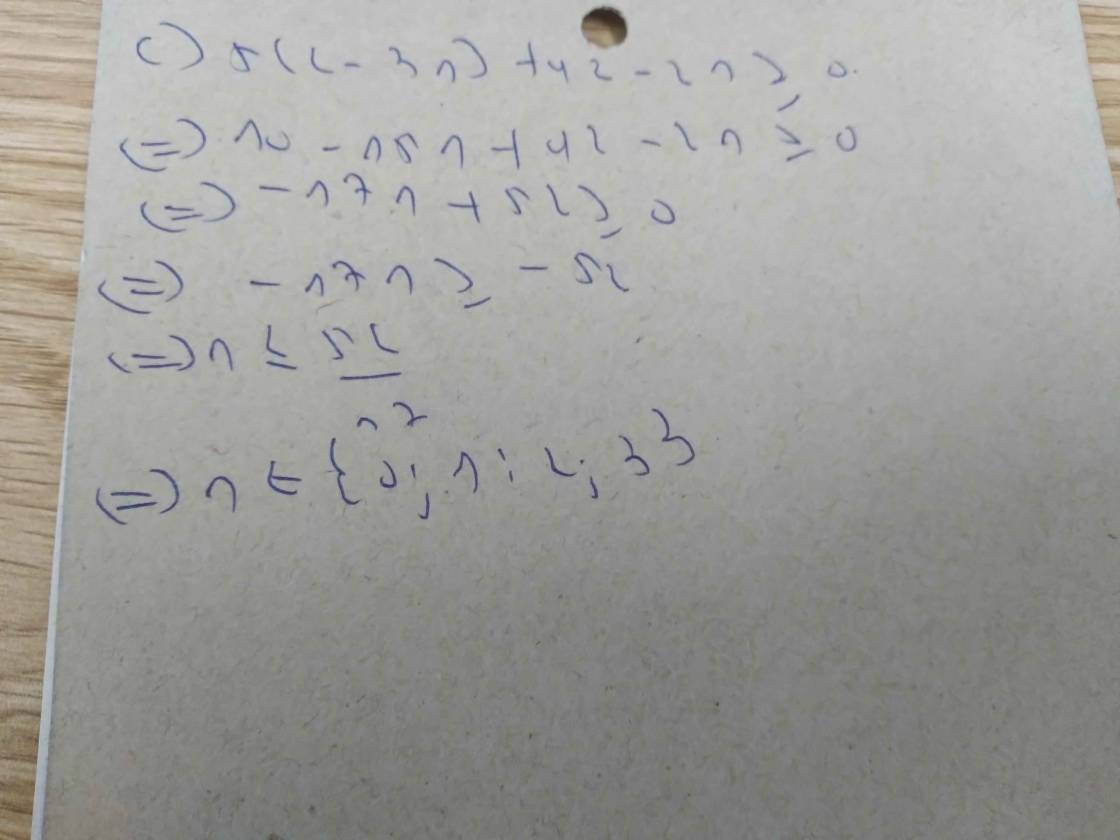tìm số tự nhiên n sao cho b. 25 < hoặc = 5^n<3125

Những câu hỏi liên quan
Chứng minh rằng :
a) n . ( n + 5 ) hoặc chia hết cho 25 hoặc không chia hết cho 5 với mọi n là các số tự nhiên.
b)( n + 2 ) . ( n + 9 ) hoặc chia hết cho 49 hoặc không chia hết cho 7 với mọi n là các số tự nhiên.
c) n2 + 5n + 4 hoặc chia hết cho 9 hoặc không chia hết cho 3 với mọi n là các số tự nhiên.
a) Nếu n = 5k => n(n+5) = 5k.(5k + 5) = 25k(k+1) chia hết cho 25
Nếu n = 5k +1 => n(n + 5) = (5k + 1).(5k+6) = 5k.5k + 5k.6 + 1.5k + 6 = (25k2 + 35k) + 6 không chia hết cho 5
Nếu n = 5k + 2 => n(n + 5) = (5k + 2)(5k + 7) = (25k2 + 35k + 10k) + 14 không chia hết cho 5
Nếu n = 5k + 3 => n(n + 5) = (5k + 3)(5k + 8) = (25k2 + 55k) + 24 không chia hết cho 5
Nếu n = 5k + 4 => n(n + 5) = (5k + 4).(5k + 9) = (25k2 + 45k + 20k) + 36 không chia hết cho 5
Vậy với mọi n thì n(n+5) hoặc chia hết cho 25 hoặc không chia hết cho 5
b,c tương tự:
Đúng 0
Bình luận (0)
Tìm số tự nhiên n sao cho 25 ≤ 5n ≤ 125
Ta có : \(25\le5^n\le125\left(n\in N\right)\)
\(\Rightarrow5^2\le5^n\le5^3\)
Do n là số tự nhiên nên, suy ra :
\(n=2;n=3\)
Đúng 0
Bình luận (0)
52 ≤ 5n ≤ 53
=> 52 ≤ 52 hay 53 ≤ 53
Vậy n = 2 và 3
Đúng 0
Bình luận (0)
có thể tìm được số tự nhiên n bé hơn hoặc bằng 2 để các số sau đây là số chính phương phải không? vì sao?
a.10^n+7
b.10^n+74
c.10^n+25
d.10^n+5
e.10^+495
a,Tìm các số tự nhiên x,y sao cho (2x +1)(y-5)=12
b/Tìm số tự nhiên n sao cho n + 5 chia hết cho n +1
c/Tìm số tự nhiên n sao cho 2n + 13 chia hết cho 2n +3
d/Tìm số tuwnhieen n sao cho 4n + 5 chia hết cho 2n +1
đặt s = 5^0 + 5^1 + 5^2 + 5^3 +...+ 5^2023
chứng minh rằng : s chia hết cho 6
tìm số tự nhiên dư sau khi s : 31
tìm số tự nhiên n sao cho 4s - 25^2n = 1
S = 5⁰ + 5¹ + 5² + ... + 5²⁰²³
= (5⁰ + 5¹) + (5² + 5³) + ... + (5²⁰²² + 5²⁰²³)
= 6 + 5².(1 + 5) + ... + 5²⁰²².(1 + 5)
= 6 + 5².6 + ... + 5²⁰²².6
= 6.(1 + 5² + ... + 5²⁰²²) ⋮ 6
Vậy S ⋮ 6
--------
Số số hạng của S:
2023 - 0 + 1 = 2024 (số)
2024 : 3 dư 2 nên khi nhóm các số hạng của S theo nhóm 3 thì dư 2 số hạng
Ta có:
S = 5⁰ + 5¹ + 5² + 5³ + ... + 5²⁰²³
= 5⁰ + 5¹ + (5² + 5³ + 5⁴) + (5⁵ + 5⁶ + 5⁷) + ... + (5²⁰²¹ + 5²⁰²² + 5²⁰²³)
= 6 + 5².(1 + 5 + 5²) + 5⁵.(1 + 5 + 5²) + ... + 5²⁰²¹.(1 + 5 + 5²)
= 6 + 5².31 + 5⁵.31 + ... + 5²⁰²¹.31
= 6 + 31.(5² + 5⁵ + ... + 5²⁰²¹)
Do 31.(5² + 5⁵ + ... + 5²⁰²¹) ⋮ 31
6 + 31.(5² + 5⁵ + ... + 5²⁰²¹) chia 31 dư 6
Vậy S chia 31 dư 6
------------
Sửa đề:
Tìm số tự nhiên n để 4S - 25² = -1
S = 5⁰ + 5¹ + 5² + 5³ + ... + 5²⁰²³
5S = 5 + 5² + 5³ + 5⁴ + ... + 5²⁰²⁴
⇒ 4S = 5S - S
= (5 + 5² + 5² + 5³ + ... + 5²⁰²⁴) - (1 + 5¹ + 5² + 5³ + ... + 5²⁰²³)
= 5²⁰²⁴ - 1
⇒ 4S - 25²ⁿ = -1
⇒ 5²⁰²⁴ - 1 - (5²)²ⁿ = -1
⇒ 5²⁰²⁴ - 5⁴ⁿ = -1 + 1
⇒ 5⁴ⁿ = 5²⁰²⁴
⇒ 4n = 2024
⇒ n = 2024 : 4
⇒ n = 506
Đúng 2
Bình luận (0)
\(S=\left(5^0+5^1\right)+\left(5^2+5^3\right)+...+\left(5^{2022}+5^{2023}\right)\\ =6+5^2\left(1+5\right)+...+5^{2022}\left(1+5\right)\\ =6+5^2.6+...+5^{2022}.6\\ =6\left(1+5^2+...+5^{2022}\right)⋮6\)
\(S=\left(5^0+5^1+5^2\right)+...+\left(5^{2021}+5^{2022}+5^{2023}\right)\\ =31+...+5^{2021}\left(1+5+5^2\right)\\ =31\left(1+...+5^{2021}\right)⋮31\)
=> Dư : 0
\(5S=5^1+5^2+5^3+5^4+...+5^{2024}\\ =>5S-S=4S=5^{2024}-1\)
Mà : \(4S-25^{2n}=1\\ =>5^{2024}-1-25^{2n}=1\\ =>5^{2024}-25^{2n}=2\)
Bạn xem lại đề nhé
Đúng 3
Bình luận (0)
bài 5 :
a, tìm số nguyên dương nhỏ nhất sao cho ; 3,6 - (1,2+0,3x) <1,8
b, tìm số nguyên âm lớn nhất sao cho : 4,1 - 2,5x > 11,6
c, tìm số tự nhiên n sao cho ; 5(2-3n) + 42 - 2n > hoặc bằng 0
Tìm số tự nhiên n ( 2010 < hoặc = n < hoặc = 2010 ) sao cho \(\sqrt{20203=21n}\)cũng là 1 số tự nhiên
Tìm số tự nhiên n sao cho biểu thức \(\sqrt{5+\sqrt{25-n}}+\sqrt{5-\sqrt{25-n}}\)có giá trị nguyên
Bạn đang tìm kiếm số tự nhiên n để biểu thức: sqrt(5 + sqrt(25 - n)) + sqrt(5 - sqrt(25 - n)) có giá trị nguyên. Để giải quyết vấn đề này, chúng ta sẽ sử dụng một số tính chất của các số nguyên và căn bậc hai.
Đầu tiên, ta nhận thấy rằng nếu biểu thức trên có giá trị nguyên, thì cả hai căn bậc hai phải là số nguyên. Điều này có nghĩa là 5 + sqrt(25 - n) và 5 - sqrt(25 - n) đều phải là bình phương của một số nguyên. Ta có thể viết lại hai biểu thức này như sau:
5 + sqrt(25 - n) = a^2 5 - sqrt(25 - n) = b^2
Trong đó a và b là các số nguyên. Từ đó, ta có:
a^2 + b^2 = 10 a^2 - b^2 = sqrt(25 - n)
Ta có thể giải hệ phương trình này để tìm a, b, và n. Đầu tiên, ta có:
(a^2 + b^2) + (a^2 - b^2) = 2a^2 = 10 + sqrt(25 - n)
Từ đó, ta suy ra:
a^2 = 5 + (1/2)sqrt(25 - n)
Tương tự, ta có:
b^2 = 5 - (1/2)sqrt(25 - n)
Do a và b là các số nguyên, ta có thể suy ra rằng sqrt(25 - n) phải là một số chẵn. Từ đó, ta có:
25 - n = 4k^2
Với k là một số nguyên. Từ đó, ta suy ra:
n = 25 - 4k^2
Vậy để biểu thức sqrt(5 + sqrt(25 - n)) + sqrt(5 - sqrt(25 - n)) có giá trị nguyên, thì n phải là một số tự nhiên sao cho sqrt(25 - n) là một số chẵn. Các giá trị của n thỏa mãn điều kiện này là n = 3 và n = 7 1.
Vì vậy, để biểu thức sqrt(5 + sqrt(25 - n)) + sqrt(5 - sqrt(25 - n)) có giá trị nguyên, thì n phải là một trong hai số tự nhiên 3 hoặc 7.
Đúng 0
Bình luận (0)
Bạn đang tìm kiếm số tự nhiên n để biểu thức: sqrt(5 + sqrt(25 - n)) + sqrt(5 - sqrt(25 - n)) có giá trị nguyên. Để giải quyết vấn đề này, chúng ta sẽ sử dụng một số tính chất của các số nguyên và căn bậc hai.
Đầu tiên, ta nhận thấy rằng nếu biểu thức trên có giá trị nguyên, thì cả hai căn bậc hai phải là số nguyên. Điều này có nghĩa là 5 + sqrt(25 - n) và 5 - sqrt(25 - n) đều phải là bình phương của một số nguyên. Ta có thể viết lại hai biểu thức này như sau:
5 + sqrt(25 - n) = a^2 5 - sqrt(25 - n) = b^2
Trong đó a và b là các số nguyên. Từ đó, ta có:
a^2 + b^2 = 10 a^2 - b^2 = sqrt(25 - n)
Ta có thể giải hệ phương trình này để tìm a, b, và n. Đầu tiên, ta có:
(a^2 + b^2) + (a^2 - b^2) = 2a^2 = 10 + sqrt(25 - n)
Từ đó, ta suy ra:
a^2 = 5 + (1/2)sqrt(25 - n)
Tương tự, ta có:
b^2 = 5 - (1/2)sqrt(25 - n)
Do a và b là các số nguyên, ta có thể suy ra rằng sqrt(25 - n) phải là một số chẵn. Từ đó, ta có:
25 - n = 4k^2
Với k là một số nguyên. Từ đó, ta suy ra:
n = 25 - 4k^2
Vậy để biểu thức sqrt(5 + sqrt(25 - n)) + sqrt(5 - sqrt(25 - n)) có giá trị nguyên, thì n phải là một số tự nhiên sao cho sqrt(25 - n) là một số chẵn. Các giá trị của n thỏa mãn điều kiện này là n = 3 và n = 7 1.
Vì vậy, để biểu thức sqrt(5 + sqrt(25 - n)) + sqrt(5 - sqrt(25 - n)) có giá trị nguyên, thì n phải là một trong hai số tự nhiên 3 hoặc 7.
Đúng 0
Bình luận (0)
Tìm số tự nhiên n biết:
a) 2n = 32
b)27 x 3n = 243
c)64 x 4n = 45
d)25 < hoặc = 5n < hoặc = 125
2n = 32
2n = 25
=> n = 5
27.3n = 243
3n = 9
3n = 32
=> n = 2
Đúng 0
Bình luận (0)