cho hình vẽ, biết AB//DE,góc OBC=50 độ,góc ODE = 140 độ.Chứng minh OB vuông góc với OD

Những câu hỏi liên quan
Cho hình vẽ: biết AB // DE; góc OBC= 50°; góc ODE= 140° Chứng minh OB vuông góc với OD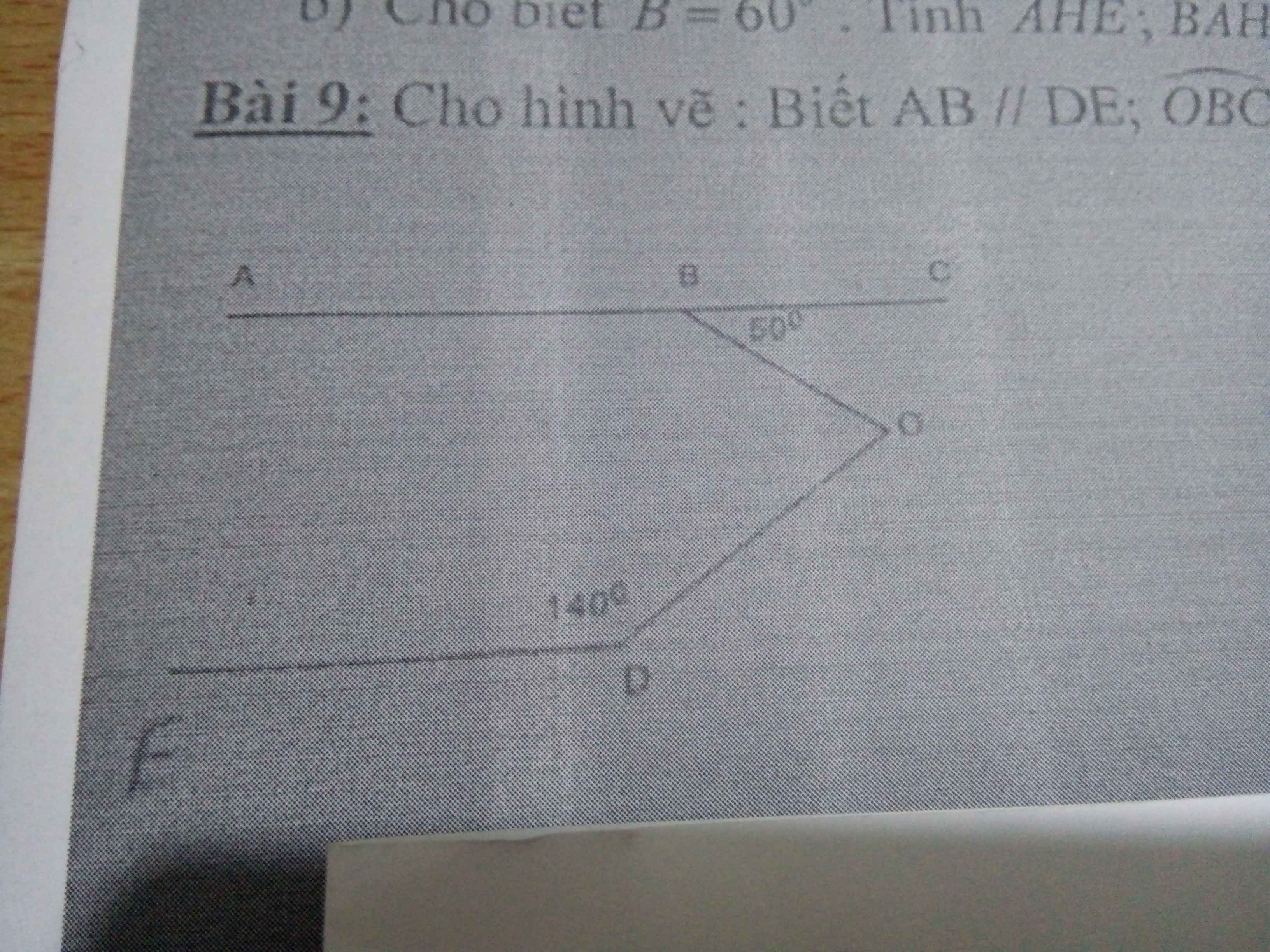
1. Cho góc AOB = 130 độ . Trong góc AOB xẽ tia OC , OD sao cho OA vuông góc OA ; OD vuông góc với OB . Tính góc COD .
2. Cho góc bẹt AOB . Trên cùng nửa mặt phẳng bờ AB . Vẽ tia OC , OD sao cho góc AOC = 40 độ ; góc BOD = 50 độ . Chứng minh OC vuông góc với OD
Đoàn Ngọc Minh Hiếu cóa roảnh
ôg lập lắm nik tek
t vô trag ôg thì ko đăng kí đc TT
Đúng 0
Bình luận (0)
Cho góc AOB=140 độ. vẽ tia OC và OD nằm giữa OA và OB sao cho OC vuông góc với OA, OD vuông góc với OB. tính góc COD
cho góc AOB= 140 độ .Trong góc AOB vẽ các tia OC ,OD sao cho OC vuông góc với OA, OD vuông góc với OB. tính COD
cho góc AOB có số đo bằng 140 độ. Tronggóc này vẽ hai tia OC và OD lần lượt vuông góc với hai tia OA và OB. So sánh AOD và góc BOC.
A. góc AOD → góc BOC B. góc AOD← góc BOC
C. góc AOD=góc BOC=50 độ D. góc AOD= góc BOC=60 độ
Cho tam giác ABC cân tại A và có góc A = 50 độ
1. tính góc B và C
2. lấy D thuộc AB,E thuộc AC sao cho AD= AE. Chứng minh DE//BC
3. Chứng minh CD=BE
4. Gọi O là giao điểm của CD và BE. Chứng minh tam giác OBC cân và tam giác ODE cân
Các bạn vẽ hình giúp mình luôn nha. Xin cảm ơn
1) Ta có: ΔABC cân tại A(gt)
nên \(\widehat{B}=\widehat{C}=\dfrac{180^0-\widehat{A}}{2}\)(Số đo của các góc ở đáy trong ΔABC cân tại A)(1)
\(\Leftrightarrow\widehat{B}=\widehat{C}=\dfrac{180^0-50^0}{2}=65^0\)
Vậy: \(\widehat{B}=65^0\); \(\widehat{C}=65^0\)
2) Xét ΔADE có AD=AE(gt)
nên ΔADE cân tại A(Định nghĩa tam giác cân)
⇒\(\widehat{ADE}=\dfrac{180^0-\widehat{A}}{2}\)(Số đo của một góc ở đáy trong ΔADE cân tại A)(2)
Từ (1) và (2) suy ra \(\widehat{ADE}=\widehat{ABC}\)
mà \(\widehat{ADE}\) và \(\widehat{ABC}\) là hai góc ở vị trí đồng vị
nên DE//BC(Dấu hiệu nhận biết hai đường thẳng song song)
3) Ta có: AD+DB=AB(D nằm giữa A và B)
AE+EC=AC(E nằm giữa A và C)
mà AB=AC(ΔABC cân tại A)
và AD=AE(gt)
nên DB=EC
Xét ΔDBC và ΔECB có
DB=EC(cmt)
\(\widehat{DBC}=\widehat{ECB}\)(cmt)
BC chung
Do đó: ΔDBC=ΔECB(c-g-c)
⇒CD=BE(hai cạnh tương ứng)
4) Ta có: ΔDBC=ΔECB(cmt)
nên \(\widehat{DCB}=\widehat{EBC}\)(hai góc tương ứng)
hay \(\widehat{OBC}=\widehat{OCB}\)
Xét ΔOBC có \(\widehat{OBC}=\widehat{OCB}\)(cmt)
nên ΔOBC cân tại O(Định lí đảo của tam giác cân)
Ta có: \(\widehat{OBC}=\widehat{OCB}\)(cmt)
mà \(\widehat{OBC}=\widehat{OED}\)(hai góc so le trong, DE//BC)
và \(\widehat{OCB}=\widehat{ODE}\)(hai góc so le trong, DE//BC)
nên \(\widehat{ODE}=\widehat{OED}\)
Xét ΔODE có \(\widehat{ODE}=\widehat{OED}\)(cmt)
nên ΔODE cân tại O(Định lí đảo của tam giác cân)
Đúng 2
Bình luận (1)
cho góc AOB =50 độ trong góc AOB vẽ các tia OC;OD sao cho OC vuông góc với OA;OD vuông góc OB tính góc COD
Cho góc AOB = 130 độ. Vẽ các tia OC, OD sao cho OC vuông góc với OA, OD vuông góc với OB.
a) Chứng minh : góc AOD = góc BOC
b) Gọi ox và oy theo thứ tự là tia phân giác của góc AOD và góc BOC. Chứng minh Ox vuông góc Oy( vẽ hình nha)
cho góc AOB bằng 140 độ ngoài góc AOB vẽ các tia OC, OD sao cho OC vuông góc với OA, OD vuông góc với OB vẽ tia OE là phân giác của góc AOB, OF là tia đối của tia OE . vì sao OF là tia phân giác của góc COD














