tìm m để đồ thị các hàm số : y=x4 - m(m+1)x2 +m3 cắt trục hoành tại bốn điểm phân biệt?
Những câu hỏi liên quan
Tìm tất cả các giá trị của tham số m để đồ thị hàm số
y
m
+
1
x
4
-
2
2
m
-
3
x
2
+
6
m
+
5
cắt trục hoành tại bốn điểm phân biệt có các hoành độ
x
1...
Đọc tiếp
Tìm tất cả các giá trị của tham số m để đồ thị hàm số y = m + 1 x 4 - 2 2 m - 3 x 2 + 6 m + 5 cắt trục hoành tại bốn điểm phân biệt có các hoành độ x 1 , x 2 , x 3 , x 4 thỏa mãn x 1 < x 2 < x 3 < 1 < x 4
A. m ∈ - 1 ; - 5 6
B. m ∈ - 3 ; - 1
C. m ∈ - 3 ; 1
D. m ∈ - 4 ; - 1
Tìm m để đồ thị hàm số: y
x
4
-
(
2
m
+
4
)
x
2
+
m
2
cắt trục hoành tại bốn điểm phân biệt có hoành độ lập thành một cấp số cộng. A. m 3, m 1 B. m 0 C. m -1 D. m 3
Đọc tiếp
Tìm m để đồ thị hàm số: y = x 4 - ( 2 m + 4 ) x 2 + m 2 cắt trục hoành tại bốn điểm phân biệt có hoành độ lập thành một cấp số cộng.
A. m = 3, m = 1
B. m = 0
C. m = -1
D. m = 3
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số
C
m
:
y
x
4
−
m
x
2
+
m
−
1
cắt trục hoành tại bốn điểm phân biệt. A.
m
1
m...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số C m : y = x 4 − m x 2 + m − 1 cắt trục hoành tại bốn điểm phân biệt.
A. m > 1 m ≠ 2
B. không có m
C. m > 1
D. m ≠ 2
Đáp án A
y ' = 4 x 3 − 2 mx
Để đồ thị cắt trục hoành tại 4 điểm phân biệt thì đồ thị hàm số phải có 3 cực trị và y C T < 0 < yCĐ Nên m>0 và y’=0 có 3 nghiệm
y ' = 0 ⇔ x= 0 x= 2 m 2 x=- 2 m 2
y C T < 0 < yCĐ ⇔ − m 2 4 + m − 1 < 0 < m − 1 ⇔ 2 ≠ m > 1
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số
C
m
:
y
x
4
−
m
x
2
+
m
−
1
cắt trục hoành tại bốn điểm phân biệt. A.
m
1
m...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số C m : y = x 4 − m x 2 + m − 1 cắt trục hoành tại bốn điểm phân biệt.
A. m > 1 m ≠ 2
B. không có m
C. m > 1
D. m ≠ 2
Đáp án A
y ' = 4 x 3 − 2 mx
Để đồ thị cắt trục hoành tại 4 điểm phân biệt thì đồ thị hàm số phải có 3 cực trị và y C T < 0 < yCĐ Nên m > 0 và y’=0 có 3 nghiệm
y ' = 0 ⇔ x= 0 x= 2 m 2 x=- 2 m 2
y C T < 0 < y C Đ ⇔ − m 2 4 + m − 1 < 0 < m − 1 ⇔ 2 ≠ m > 1
Đúng 0
Bình luận (0)
Cho hàm số y=x4-(3m+4) x2+ m2 có đồ thị là C. Có mấy giá trị nguyên của m để đồ thị C cắt trục hoành tại bốn điểm phân biệt có hoành độ lập thành một cấp số cộng.
A. 0
B. 1
C. 2
D. 3
Phương trình hoành độ giao điểm: x4-(3m+4) x2+ m2 = 0 ( 1)
Đặt t= x2, phương trình trở thành: t2-(3m+4)t+ m2 = 0 ( 2)
C cắt trục hoành tại bốn điểm phân biệt khi và chỉ khi ( 1) có bốn nghiệm phân biệt
Khi đó ( 2) có hai nghiệm dương phân biệt
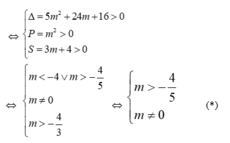
+ Khi đó phương trình *(2) có hai nghiệm 0<t1< y2. Suy ra phương trình (1) có bốn nghiệm phân biệt là x 1 = - t 2 < x 2 = - t 1 < x 3 = t 1 < x 4 = - t 2 . Bốn nghiệm x1; x2; x3; x4 lập thành cấp số cộng
⇔ x 2 - x 1 = x 3 - x 2 = x 4 - x 3 ⇔ - t 1 + t 2 = 2 t 1 ⇔ t 2 = 3 t 1 ⇔ t 2 = 9 t 1 ( 3 )
Theo định lý Viet ta có t 1 + t 2 = 3 m + 4 ( 4 ) t 1 t 2 = m 2 ( 5 )
Từ (3) và (4) ta suy ra được t 1 = 3 m + 4 10 t 2 = 9 ( 3 m + 4 ) 10 ( 6 ) .
Thay (6) vào (5) ta được
Vậy giá trị m cần tìm làm =12; m= -12/ 19
Chọn B.
Đúng 0
Bình luận (0)
Cho hàm số y= x4-(3m+4)x2+m2 có đồ thị là (C). Có mấy giá trị nguyên của m để đồ thị (C) cắt trục hoành tại bốn điểm phân biệt có hoành độ lập thành một cấp số cộng.
A: 0
B: 1
C: 2
D: 3
Phương trình hoành độ giao điểm: x4-(3m+4)x2+m2 =0 (1)
Đặt t = x2 ≥ 0, phương trình (1) trở thành: t2-(3m+4)t+m2=0 (2)
(C) cắt trục hoành tại bốn điểm phân biệt khi (1) có bốn nghiệm phân biệt
Hay (2) có hai nghiệm dương phân biệt
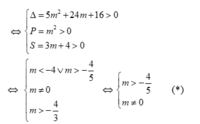
Khi đó phương trình (2) có hai nghiệm 0<t1<t2 Suy ra phương trình (1) có bốn nghiệm phân biệt là 
Bốn nghiệm x1; x2 ; x3; x4 lập thành cấp số cộng
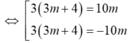
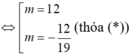
Vậy giá trị m cần tìm là m=12; m=-12/19; có 1 giá trị nguyên của m thỏa mãn yêu cầu đề bài.
Chọn B.
Đúng 0
Bình luận (0)
Cho đồ thị hàm số
C
:
y
x
4
-
(
3
m
+
1
)
x
2
+
m
2
(m là tham số). Để (C) cắt trục hoành tại bốn phân biệt có hoành độ lập thành cấp số cộng thì giá trị của m là:
Đọc tiếp
Cho đồ thị hàm số C : y = x 4 - ( 3 m + 1 ) x 2 + m 2 (m là tham số). Để (C) cắt trục hoành tại bốn phân biệt có hoành độ lập thành cấp số cộng thì giá trị của m là:
Cho đồ thị hàm số
(
C
)
:
y
x
4
-
(
3
m
+
1
)
x
2
+
m
2
(m là tham số). Để (C) cắt trục hoành tại bốn phân biệt có hoành độ lập thành cấp số cộng thì giá trị của m là: A.
m
-
1
5...
Đọc tiếp
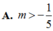
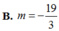
Cho đồ thị hàm số ( C ) : y = x 4 - ( 3 m + 1 ) x 2 + m 2 (m là tham số). Để (C) cắt trục hoành tại bốn phân biệt có hoành độ lập thành cấp số cộng thì giá trị của m là:
A. m > - 1 5
B. m = - 19 3
C. m=3
D. m = 3 , m = - 3 19
Cho hàm số
y
x
4
-
2
(
2
m
+
1
)
x
2
+
4
m
2
(
1
)
. Các giá trị của tham số m để đồ thị hàm số (1) cắt trục hoành tại 4 điểm phân biệt có hoành độ
x
1
,
x
2
,
x
3
,
x
4
...
Đọc tiếp
Cho hàm số y = x 4 - 2 ( 2 m + 1 ) x 2 + 4 m 2 ( 1 ) . Các giá trị của tham số m để đồ thị hàm số (1) cắt trục hoành tại 4 điểm phân biệt có hoành độ x 1 , x 2 , x 3 , x 4 thỏa mãn là x 1 2 + x 2 2 + x 3 2 + x 4 2 = 6
A. m = 1 4
B. m > - 1 2
C. m > - 1 4
D. m ≥ - 1 4
Cho hàm số
y
x
4
-
m
-
1
x
2
+
m
-
2
. Tìm m để đồ thị hàm số cắt trục hoành tại 4 điểm phân biệt. A. mÎ(1; +¥) B. mÎ(2; +¥ ) C. mÎ(2; +¥) {3} D. mÎ(2;3)
Đọc tiếp
Cho hàm số y = x 4 - m - 1 x 2 + m - 2 . Tìm m để đồ thị hàm số cắt trục hoành tại 4 điểm phân biệt.
A. mÎ(1; +¥)
B. mÎ(2; +¥ )
C. mÎ(2; +¥) \{3}
D. mÎ(2;3)
