Tìm GTNN của
B=x^4-32x ( với x>=0)
mn giúp em vs ak. em đang cần gấp
Tìm GTNN của B=(x2+x)2+4(x2+x)-12
Mọi ng giúp em với em đang cần gấp ạ. Em cảm ơn
\(B=\left(x^2+x\right)^2+4\left(x^2+x\right)+4-16=\left(x^2+x+2\right)^2-16\ge-16\)
Dấu \("="\Leftrightarrow x^2+x+2=0\Leftrightarrow x\in\varnothing\left(x^2+x+2>0\right)\)
Vậy dấu \("="\) ko xảy ra nên sẽ ko tính đc GTNN
\(B=\left(x^2+x\right)^2+4\left(x^2+x^2\right)-12\)
\(=\left(x^2+x\right)^2+4\left(x^2+x\right)+4-16\)
\(=\left(x^2+x+2\right)^2-16\)
\(=\left[\left(x+\dfrac{1}{2}\right)^2+\dfrac{7}{4}\right]^2-16\)
Do \(\left(x+\dfrac{1}{2}\right)^2\ge0;\forall x\Rightarrow\left(x+\dfrac{1}{2}\right)^2+\dfrac{7}{4}\ge\dfrac{7}{4}\)
\(\Rightarrow B\ge\left(\dfrac{7}{4}\right)^2-16=-\dfrac{207}{16}\)
\(B_{min}=-\dfrac{207}{16}\) khi \(x=-\dfrac{1}{2}\)
Cho 3 số a,b,c dương thỏa mãn (a+b)(a+c)=8.
Tìm GTLN của biểu thức A=abc(a+b+c)
MN giúp em bài này vs ak. rồi em tick luôn cho ak...em đang cần gấp, mong mn giúp ạ!
( a + b ) ( a + c ) = 8 hay a2 + ab + ac + bc = 8
\(\Rightarrow\)a ( a + b + c ) + bc = 8
\(\sqrt{abc\left(a+b+c\right)}=\sqrt{a\left(a+b+c\right).bc}\le\frac{a\left(a+b+c\right)+bc}{2}=4\)
\(\Rightarrow abc\left(a+b+c\right)\le16\)
Vậy GTLN của A là 16
cho x,y>0,Tìm GTNN của A=\(\sqrt{\dfrac{x^3}{x^3+8y^3}}+\sqrt{\dfrac{4y^3}{y^3+\left(x+y\right)^3}}\)
MN giúp em với em cần gấp ạ
Lời giải:
\(A=\frac{x^2}{\sqrt{x^4+8xy^3}}+\frac{2y^2}{\sqrt{y^4+y(x+y)^3}}\)
Xét:
\(x^4+8xy^3-(x^2+2y^2)^2=8xy^3-4y^4-4x^2y^2\)
\(=-4y^2(x^2-2xy+y^2)=-4y^2(x-y)^2\leq 0\)
\(\Rightarrow x^4+8xy^3\leq (x^2+2y^2)^2\)
\(\Rightarrow \frac{x^2}{\sqrt{x^4+8xy^3}}\geq \frac{x^2}{x^2+2y^2}(*)\)
Mặt khác:
\(y^4+y(x+y)^3-(x^2+2y^2)^2=x^3y+3xy^3-2y^4-x^4-x^2y^2\)
\(=x^3(y-x)+3y^3(x-y)+y^4-x^2y^2\)
\(=x^3(y-x)+3y^3(x-y)+y^2(y-x)(y+x)\)
\(=(y-x)(x^3-2y^3+xy^2)\)
\(=(y-x)[(x-y)(x^2+xy+y^2)+y^2(x-y)]\)
\(=-(x-y)^2(x^2+xy+2y^2)\leq 0\)
\(\Rightarrow y^4+y(x+y)^3\leq (x^2+2y^2)^2\Rightarrow \frac{2y^2}{\sqrt{y^4+y(x+y)^3}}\geq \frac{2y^2}{x^2+2y^2}(**)\)
Từ $(*); (**)\Rightarrow A\geq 1$
Tìm GTNN của biểu thức Q= \(\sqrt{x-1}-12\)
GIÚP EM VỚI Ạ EM ĐANG CẦN GẤP Ạ
đk : x>= 1
Q = \(\sqrt{x-1}-12\)
với \(x\ge1\Leftrightarrow x-1\ge0\Leftrightarrow\sqrt{x-1}\ge0\Leftrightarrow\sqrt{x-1}-12\ge12\)
Dấu ''='' xảy ra khi x = 1
tìm GTLN của P=((3*căn x)+8)/((căn x)+2)
mn giúp mình vs ak . mình đang cần gấp.
GTLN ak. bạn có nhầm đề k vậy, bạn xem lại đề đi.
mình k ak
bạn giúp mình phân tích cái kia ra là đc
k tìm dc GTLN nhà bạn, bạn xem lại đề đi
Giúp em bài 4 vs ak em đang cần gấp lm ak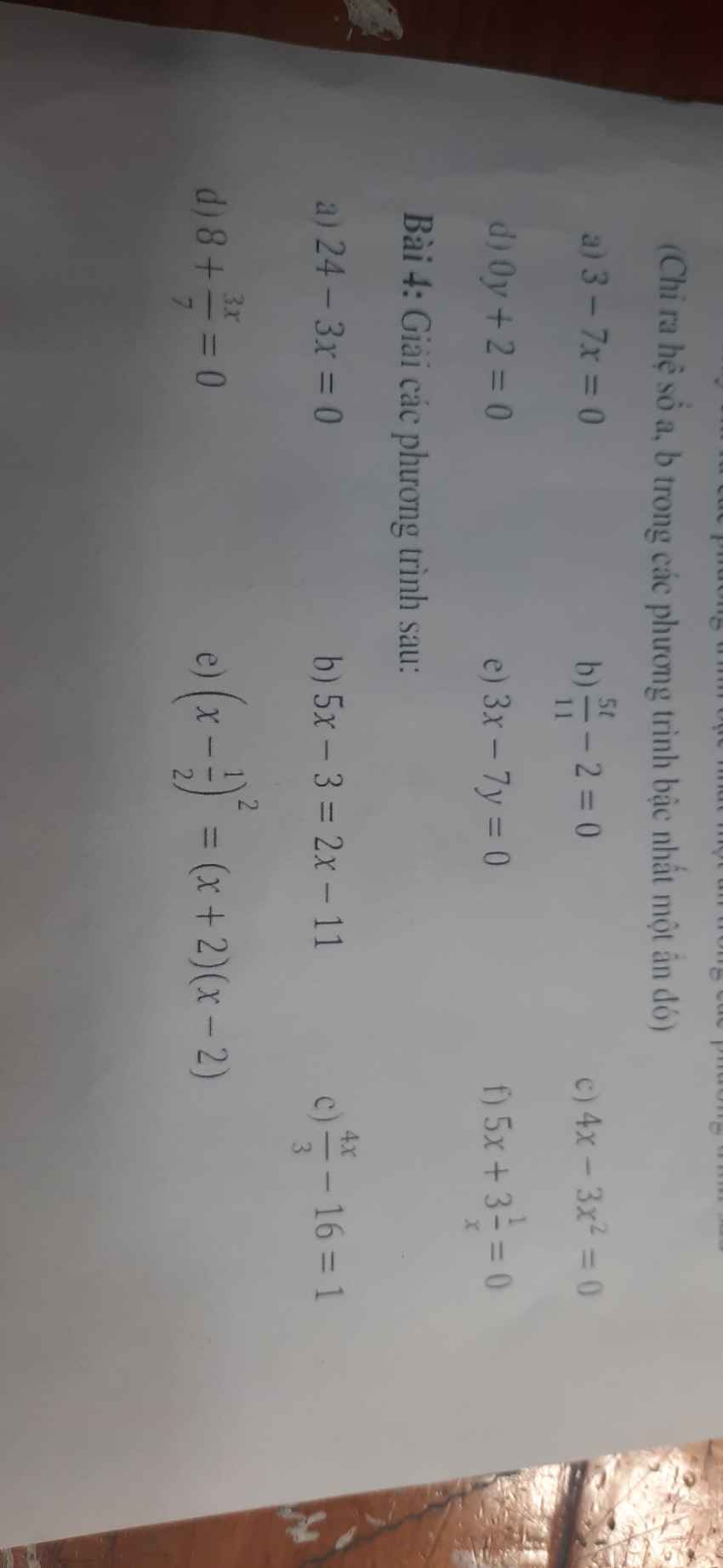
Bài 4:
a: =>3x=24
hay x=8
b: =>5x-2x=-11+3
=>3x=-8
hay x=-8/3
c: =>4/3x=17
hay x=51/4
d: =>3/7x=-8
hay x=-56/3
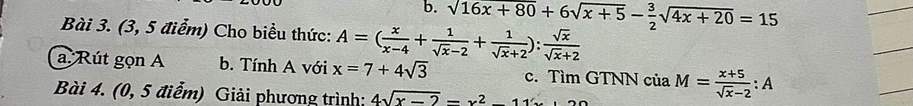 mn giúp em phần tìm gtnn vs ạ, em cần gấp
mn giúp em phần tìm gtnn vs ạ, em cần gấp
a) Ta có: \(A=\left(\dfrac{x}{x-4}+\dfrac{1}{\sqrt{x}-2}+\dfrac{1}{\sqrt{x}+2}\right):\dfrac{\sqrt{x}}{\sqrt{x}+2}\)
\(=\dfrac{x+\sqrt{x}+2+\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\cdot\dfrac{\sqrt{x}+2}{\sqrt{x}}\)
\(=\dfrac{x+2\sqrt{x}}{\sqrt{x}-2}\cdot\dfrac{1}{\sqrt{x}}\)
\(=\dfrac{\sqrt{x}+2}{\sqrt{x}-2}\)
b) Thay \(x=7+4\sqrt{3}\) vào A, ta được:
\(A=\dfrac{2+\sqrt{3}+2}{2+\sqrt{3}-2}=\dfrac{4+\sqrt{3}}{\sqrt{3}}=\dfrac{4\sqrt{3}+3}{3}\)
c) Ta có: \(M=\dfrac{x+5}{\sqrt{x}-2}:\dfrac{\sqrt{x}+2}{\sqrt{x}-2}\)
\(=\dfrac{x+5}{\sqrt{x}-2}\cdot\dfrac{\sqrt{x}-2}{\sqrt{x}+2}\)
\(=\dfrac{x+5}{\sqrt{x}+2}\)
\(=\sqrt{x}+2+\dfrac{9}{\sqrt{x}+2}-4\)
\(\Leftrightarrow M\ge2\cdot\sqrt{\left(\sqrt{x}+2\right)\cdot\dfrac{9}{\sqrt{x}+2}}-4\)
\(\Leftrightarrow M\ge2\cdot3-4=6-4=2\)
Dấu '=' xảy ra khi \(\sqrt{x}+2=3\)
\(\Leftrightarrow\sqrt{x}=1\)
hay x=1
Giúp mik vs Tìm gtnn của: A=|x+1|+|x+2|x-4| Mik cần gấp mn ơi
$|x+2|x-4|$ nghĩa là gì thế bạn? Bạn coi lại đề.
OK. Theo đề bạn sửa thì làm như sau:
Áp dụng BĐT dạng $|a|+|b|\geq |a+b|$ ta có:
$|x+2|+|x-4|=|x+2|+|4-x|\geq |x+2+4-x|=6$
$|x+1|\geq 0$ (theo tính chất trị tuyệt đối)
Do đó: $A\geq 6+0=6$
Vậy GTNN của $A$ là $6$ khi $(x+2)(4-x)\geq 0$ và $x+1=0$
Hay $x=-1$
Giúp em vs!
| x.4/15 | - | -3,75 | = -| -2,15|
Giải theo cách làm của lớp 7 nha mn: có 2 trường hợp ....>hoặc=0 ...... <0
Mong ACE giúp đỡ, em đang cần kết quả gấp.
Xin cảm ơm mn rất nhiều!
\(\left|x.\frac{4}{15}\right|-\left|-3,75\right|=-\left|-2,15\right|\)
\(\Rightarrow\left|x.\frac{4}{15}\right|-3,75=-2,15\)
\(\Rightarrow\left|x.\frac{4}{15}\right|=-2,15+3,75\)
\(\Rightarrow\left|x.\frac{4}{15}\right|=1,5\)
\(\Rightarrow\orbr{\begin{cases}x.\frac{4}{15}=1,5\\x.\frac{4}{15}=-1,5\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}x=\frac{45}{8}\\x=-\frac{45}{8}\end{cases}}\)
Có phải theo cách của em là làm như này đúng ko ah Bảo Bình
| X+4/15| - |3,75| = -| -2,25|
=> |x+4/15| - 3,75 = -2.25
+ x+4/15> hoặc =0 =>|x+4/15|=x+4/15
=>x+4/15 - 3,75 = -2.25
x+4/15=1.5
x=45/8
+ x+4/15<0 => |x+4/15|=-(x+4/15)
=> -(x+4/15) - 3.75 = -2,25
-x+4/15=1.5
-x=48/5
=> x=-45/8