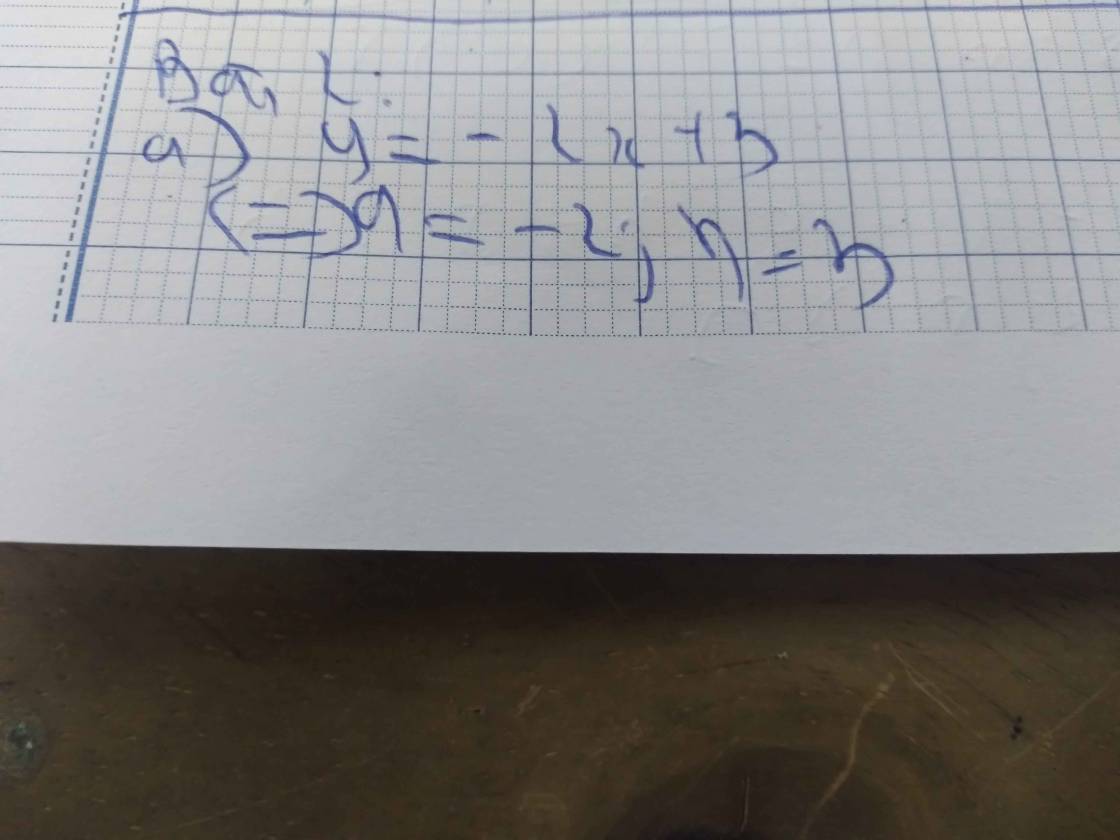
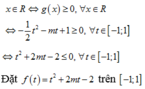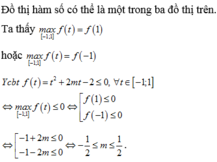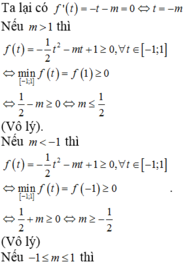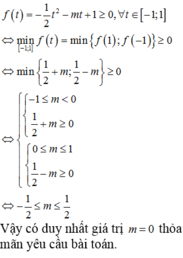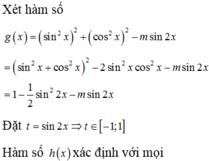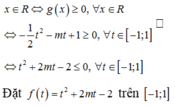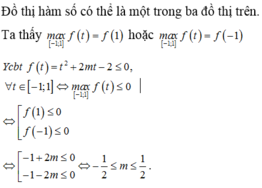Tìm m để hàm số \(y=\sqrt{5\sin4x-6\cos4x+2m-1}\) xác định \(\forall x\)

Những câu hỏi liên quan
Tìm tham số m để hàm số sau xác định trên R
1/ y√cos2x+cosx−2m+1
2/ y√cos2x−2cosx+m����2�−2����+�
3/ y√sin4x+cos4x−sin2x−m
Đọc tiếp
Tìm tham số m để hàm số sau xác định trên R
1/
3/
Tìm tham số m để hàm số sau xác định trên R1/ y√cos2x+cosx−2m+1����2�+����−2�+12/ y√cos2x−2cosx+m����2�−2����+�3/ y√sin4x+cos4x−sin2x−m
Đọc tiếp
Tìm tham số m để hàm số sau xác định trên R
1/
2/
3/
Để hàm số y xác định trên R, ta cần xác định điều kiện để biểu thức trong dấu căn không âm: 1/ y = √(cos^2x + cosx - 2m + 1) Điều kiện: cos^2x + cosx - 2m + 1 ≥ 0 - Để giải bất phương trình này, ta cần tìm giá trị của m sao cho đa thức bậc 2: f(x) = cos^2x + cosx - 2m + 1 không có nghiệm trong khoảng [-∞ , +∞]. - Để f(x) không có nghiệm, ta cần xét delta của đa thức: Δ = b^2 - 4ac = 1 - 4(1)(-2m + 1) = 8m - 3 - Để f(x) không có nghiệm, ta cần Δ < 0: 8m - 3 < 0 => m < 3/8 Do đó, hàm số y = √(cos^2x + cosx - 2m + 1) xác định trên R khi m < 3/8. 2/ y = √(cos^2x - 2cosx + m) Điều kiện: cos^2x - 2cosx + m ≥ 0 - Để giải được bất phương trình này, ta cần tìm giá trị của m sao cho đa thức bậc 2: f(x) = cos^2x - 2cosx + m không có nghiệm trong khoảng [-∞, +∞]. - Để f(x) không có nghiệm, ta cần xét delta của đa thức: Δ = b^2 - 4ac = (-2)^2 - 4(1)(m) = 4 - 4m = 4(1 - m) ) - Để f(x) không có nghiệm, ta cần Δ < 0: 1 - m < 0 => m > 1 Do đó, hàm số y = √(cos^2x - 2cosx + m) xác định trên R khi m > 1. 3/ y = √(sin^4x + cos^4x - sin^2x - m) Điều kiện: sin^4x + cos^4x - sin^2x - m ≥ 0 - Để giải được bất phương trình này, ta cần tìm giá trị của m sao cho đa thức bậc 4: f(x) = sin^4x + cos^4x - sin^2x - m không có nghiệm trong khoảng [-∞, +∞]. - Để f(x) không có nghiệm, ta cần xét delta của đa thức: Δ = b^2 - 4ac = (-1)^2 - 4(1)(-m) = 1 + 4m - Để f(x) ) không có nghiệm, ta cần Δ < 0: 4m < -1 => m < -1/4 Do đó, hàm số y = √(sin^4x + cos^4x - sin^2x - m) xác định trên R khi m < -1/4.
Đúng 0
Bình luận (0)
Cho hàm số h(x)
sin
4
x
+
cos
4
x
-
2
m
sin
x
.
cos
x...
Đọc tiếp
Cho hàm số h(x) = sin 4 x + cos 4 x - 2 m sin x . cos x . Có bao nhiêu giá trị nguyên của tham số m để hàm số xác định với mọi x ∈ R
A. 1
B. 2
C. 3
D. 4
Cho hàm số h(x)
sin
4
x
+
cos
4
x
-
2
m
sin
x
.
cos
x
Có bao nhiêu giá trị nguyên của tham số m để hàm số xác định với mọi
x
∈
R
A....
Đọc tiếp
Cho hàm số h(x)= sin 4 x + cos 4 x - 2 m sin x . cos x Có bao nhiêu giá trị nguyên của tham số m để hàm số xác định với mọi x ∈ R
A. 1
B. 2
C.3
D. 4
Chọn A
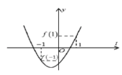
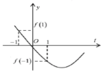
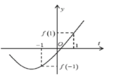
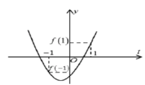
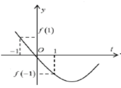
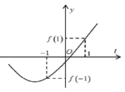
Xét hàm số
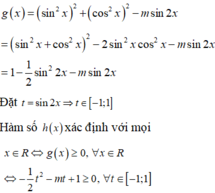
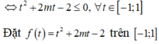
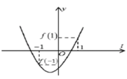
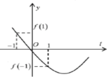
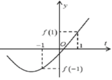
Đồ thị hàm số có thể là một trong ba đồ thị trên.
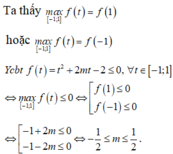
Đúng 0
Bình luận (0)
Cho hàm số
h
x
sin
4
x
+
cos
4
x
-
2
m
sin
x
cos
x
. Có bao nhiêu giá trị nguyên của tham số m để hàm số xác định với mọi
x
∈
ℝ
A. 1 B. 2 C. 3 D. 4
Đọc tiếp
Cho hàm số h x = sin 4 x + cos 4 x - 2 m sin x cos x . Có bao nhiêu giá trị nguyên của tham số m để hàm số xác định với mọi x ∈ ℝ
A. 1
B. 2
C. 3
D. 4
Chọn A.
Phương pháp: Giải và biện luận điều kiện xác định.
Cách giải: Để hàm số xác định với mọi x ∈ ℝ thì
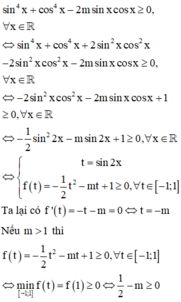
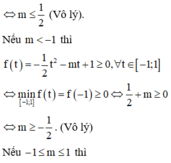
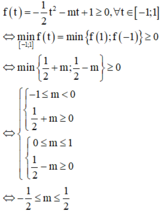
Vậy có duy nhất giá trị m = 0 thỏa mãn yêu cầu bài toán.
Đúng 0
Bình luận (0)
Cho hàm số
h
x
sin
4
x
+
cos
4
x
-
2
m
sin
x
cos
x
. Có bao nhiêu giá trị nguyên của tham số m để hàm số xác định với mọi
x
∈
ℝ
A. 1 B. 2 C. 3 D. 4
Đọc tiếp
Cho hàm số h x = sin 4 x + cos 4 x - 2 m sin x cos x . Có bao nhiêu giá trị nguyên của tham số m để hàm số xác định với mọi x ∈ ℝ
A. 1
B. 2
C. 3
D. 4
Cho hàm số
h
(
x
)
sin
4
x
+
c
o
s
4
x
-
2
m
.
sin
x
.
...
Đọc tiếp
Cho hàm số h ( x ) = sin 4 x + c o s 4 x - 2 m . sin x . cos x . Có bao nhiêu giá trị nguyên của tham số m để hàm số xác định với mọi x ∈ R .
A. 1
B. 2
C. 3
D. 4
1, Cho hàm số y=\(\sqrt{x-2m+1}\) .Tìm m để hàm số xác định trên (2 ;+∞)
Bài 1: Tìm m để các hàm số sau là hàm số bậc nhất a) y ( m - 2 )x - dfrac{2}{3} b) y ( 4 - 2022m )x - 2 c) y sqrt{1-2m}x + m - 3Bài 2: Cho đồ thị hàm số y -2x + 3a) Xác định hệ số a,bb) Các điểm A( -2 ; 7) ; B(sqrt{2} ; 6)c) Tìm tọa độ điểm M thuộc ( d ) có tung độ 11d) Tìm tọa độ điểm C thuộc ( d ), biết rằng hoành độ của điểm C gấp 3 tung độ của nóe) Tìm tọa độ điểm E thuộc ( d ), biết rằng tung độ của điểm E và hoành độ là 2 số đối nhau
Đọc tiếp
Bài 1: Tìm m để các hàm số sau là hàm số bậc nhất
a) y= ( m - 2 )x - \(\dfrac{2}{3}\) b) y= ( 4 - 2022m )x - 2 c) y= \(\sqrt{1-2m}\)x + m - 3
Bài 2: Cho đồ thị hàm số y= -2x + 3
a) Xác định hệ số a,b
b) Các điểm A( -2 ; 7) ; B(\(\sqrt{2}\) ; 6)
c) Tìm tọa độ điểm M thuộc ( d ) có tung độ = 11
d) Tìm tọa độ điểm C thuộc ( d ), biết rằng hoành độ của điểm C gấp 3 tung độ của nó
e) Tìm tọa độ điểm E thuộc ( d ), biết rằng tung độ của điểm E và hoành độ là 2 số đối nhau