Giúp mình câu này với
3cosx.(1-cos2x)+2sin2x+sinx+cos2x=0
giải phương trình: 3cosx(1 - cos2x) + 2sin2x + sinx + cos2x = 0
cos2x = 1- sin^x
sin2x= 2sinxcosx
Nhóm lại bình thường và giải thôi
a, cos3x + cos2x - cosx - 1 = 0
b, cos(8sinx) = 1
c, 1 + cos2x + cosx = 0
d, 3cosx + |sinx| = 2
a/
\(\Leftrightarrow4cos^3x-3cosx+2cos^2x-1-cosx-1=0\)
\(\Leftrightarrow2cos^3x+cos^2x-2cosx-1=0\)
\(\Leftrightarrow cos^2x\left(2cosx+1\right)-\left(2cosx+1\right)=0\)
\(\Leftrightarrow\left(cos^2x-1\right)\left(2cosx+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=0\\2cosx+1=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=0\\cosx=-\frac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=k\pi\\x=\pm\frac{2\pi}{3}+k2\pi\end{matrix}\right.\)
b/
\(cos\left(8sinx\right)=1\)
\(\Leftrightarrow8sinx=k2\pi\)
\(\Leftrightarrow sinx=\frac{k\pi}{4}\)
Do \(-1\le sinx\le1\Rightarrow-1\le\frac{k\pi}{4}\le1\)
\(\Rightarrow k=\left\{-1;0;1\right\}\)
\(\Rightarrow\left[{}\begin{matrix}sinx=-\frac{\pi}{4}\\sinx=0\\sinx=\frac{\pi}{4}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\pm arcsin\left(\frac{\pi}{4}\right)+k2\pi\\x=\pi\pm arcsin\left(\frac{\pi}{4}\right)+k2\pi\\x=k\pi\end{matrix}\right.\)
c/
\(\Leftrightarrow1+2cos^2x-1+cosx=0\)
\(\Leftrightarrow2cos^2x-cosx=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=0\\cosx=\frac{1}{2}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\frac{\pi}{2}+k\pi\\x=\pm\frac{\pi}{3}+k2\pi\end{matrix}\right.\)
d/
Đặt \(\left\{{}\begin{matrix}\left|sinx\right|=a\ge0\\cosx=b\end{matrix}\right.\) ta được hệ:
\(\left\{{}\begin{matrix}a+3b=2\\a^2+b^2=1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=2-3b\\a^2+b^2=1\end{matrix}\right.\)
\(\Rightarrow\left(2-3b\right)^2+b^2-1=0\)
\(\Rightarrow10b^2-12b+3=0\Rightarrow\left[{}\begin{matrix}b=\frac{6+\sqrt{6}}{10}\Rightarrow a=\frac{2-3\sqrt{6}}{10}\left(l\right)\\b=\frac{6-\sqrt{6}}{10}\Rightarrow a=\frac{2+3\sqrt{6}}{10}\end{matrix}\right.\)
\(\Rightarrow cosx=\frac{6-\sqrt{6}}{10}\)
\(\Rightarrow x=\pm arccos\left(\frac{6-\sqrt{6}}{10}\right)+k2\pi\)
Câu 1: Tính tổng tất cả các nghiệm của phương trình sin3(\(x-\dfrac{\pi}{4}\)) = \(\sqrt{2}\)sinx trên đoạn [0 ; 2018]
Câu 2: Tính tổng tất cả các nghiệm của phương trình cos2x (tan2x - cos2x) = cos3x - cos2x + 1 trên đoạn [0 ; 43π]
GIÚP MÌNH VỚI!!!![]()
Phương trình 2 sin 2 x + sin x cos x - cos 2 x = 0 có nghiệm là:
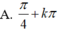


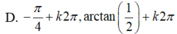
Phương trình 2sin2x + sinx. cosx – cos2x = 0 có nghiệm là:
![]()

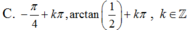
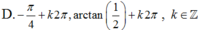
Hướng dẫn giải
Chọn C.
TH1: Nếu cosx =0 có sin2x = 1 không thỏa mãn phương trình.
TH2: ![]() chia cả hai vế của phương trình cho cos2x ta được:
chia cả hai vế của phương trình cho cos2x ta được:
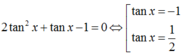
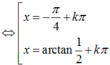
1> 1 + sinx + cosx + sin2x + cos2x = 0
2> cos2x + 3sin2x + 5 sinx - 3cosx = 3
3> \(\dfrac{\sqrt{2}*(cosx - sinx)}{cotx - 1}\) = \(\dfrac{1}{tanx + cot2x}\)
4> (2cosx - 1)*(2sinx + cosx) = sin2x - sinx
giải phương trình \(\dfrac{cos2x+3cosx+1}{sinx+1}=-1\)
@Nguyễn Việt Lâm anh giải bài này như nào ạ, cách của em nó dài mất hơn nữa mặt giấy '^^
ĐKXĐ: ...
\(\Leftrightarrow cos2x+3cosx+1=-sinx-1\)
\(\Leftrightarrow cos2x+3cosx+sinx+2=0\)
\(\Leftrightarrow cos^2x-sin^2x+3cosx+sinx+2=0\)
\(\Leftrightarrow\left(cosx-sinx\right)\left(cosx+sinx\right)+cosx-sinx+2cosx+2sinx+2=0\)
\(\Leftrightarrow\left(cosx-sinx\right)\left(cosx+sinx+1\right)+2\left(cosx+sinx+1\right)=0\)
\(\Leftrightarrow\left(cosx-sinx+2\right)\left(cosx+sinx+1\right)=0\)
\(\Leftrightarrow...\)
Giải các phương trình sau:
a, cos3x-4cos2x+3cosx-4=0, ∀x∈[0;14]
b, (2cosx-1)(2cos+cosx)=sin2x-sinx
c, cos3x+cos2x+1+sin2x+cos2x=0
@Nguyễn Việt Lâm giúp em với ạ
a/ \(4cos^3x-3cosx-4\left(2cos^2x-1\right)+3cosx-4=0\)
\(\Leftrightarrow4cos^3x-8cos^2x=0\)
\(\Leftrightarrow4cos^2x\left(cosx-2\right)=0\)
\(\Leftrightarrow cosx=0\Rightarrow x=\frac{\pi}{2}+k\pi\)
\(0< \frac{\pi}{2}+k\pi< 14\Rightarrow-\frac{1}{2}< k< \frac{14-\frac{\pi}{2}}{\pi}\Rightarrow k=\left\{0;1;2;3\right\}\)
\(\Rightarrow x=\left\{\frac{\pi}{2};\frac{3\pi}{2};\frac{5\pi}{2};\frac{7\pi}{2}\right\}\)
b/ Bạn coi lại đề, cái ngoặc thứ 2 thiếu \(\left(2cos\left(???\right)+cosx\right)\)
c/ Bạn coi lại đề, có 2 số hạng \(cos2x\) xuất hiện ở vế trái, cấp 3 chắc ko ai cho kiểu vậy đâu, nếu đúng thế thì người ta cộng luôn thành \(2cos2x\) cho rồi
sin^3 x +cos^3 x -3sinx cosx+1=0
3 cosx -3sin2x= √3(cos2x+sinx)
4sin^3x +3sin^2x cosx -sinx-cos^3x=0
√3sin4x-cos4x=sinx- √3cosx
m.n giúp mk chứng minh với ạ