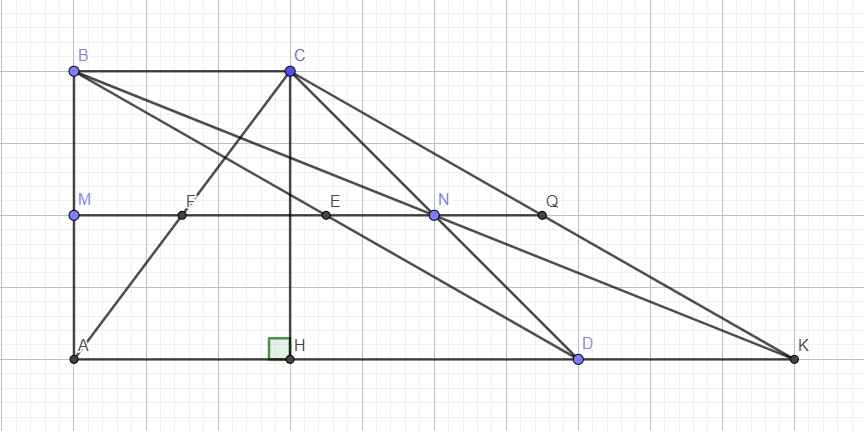
Cho hình thang vuôn ABCD. AB cắt CD tại K . Gọi N là trung điểm AD, M là tđ BD .Cm K,M,N thẳng hàng

Những câu hỏi liên quan
Cho hình thang ABCD (AB//CD). M là trung điểm của CD. AM cắt BD tại I. BM cắt AC tại K. KI cắt BD, BC lần lượt tại E là F. Gọi N là trung điểm của AB, O là giao điểm của AC và BD. Chứng minh M, O, N thẳng hàng.
Cho hình thang ABCD (AB // CD), đáy AB = 2CD. Hai tia AD và BC cắt nhau tại I. Gọi M,N lần lượt là trung điểm của AB, CD và K là giao điểm của hai đường chéo AC, BD. Chứng minh:
a) Tứ giác ADCM, BCDM, CIDM là hình thang.
b) Bốn điểm M, N, I, K thẳng hàng
Cần gấp ạ!
cho hình thang abcd (ab//cd). gọi k, l lần lượt là trung điểm của ab và cd. gọi s là điểm bất kì trên tia đối của tia bd. đường thẳng SK cắt AD tại M và đường thẳng SL cắt AB tại N. CMR MN//AB
cho hình thang ABCD, AB//CD. M là trung điểm của CD, I là giao điểm của AM và BD; K là giao điểm của BM và AC. gọi O là giao điểm AC và BD.MO cắt AB tại N; BO cắt BC tại S. CMR: N là trung điểm của AB. A;D;S thẳng hàng
Cho hình thang cân ABCD có AB//CD và AB<CD. Gọi O là giao của 2 cạnh bên. CMR. Tam giác OAB cân
b,Gọi I là trung điểm của AB, K là trung điểm của CD . CM O,I,K thẳng hàng
c,TỪ M thuộc AD, kẻ đường thẳng song song với DC cắt BC ở N. CM MNCD là hình thang cân
xét hình thang cân ABCD có AB//CD(gt)
\(\Rightarrow\)^CDA=^BAO(2 góc đồng vị) và ^DCB=^ABO
Do ABCD là hìng thang cân nên ^CDA=^DCB
nên ^BAO=^ABO
Xét tam giác ABO có
^BAO=^ABO nên tam giác ABO cân(đpcm)
Đúng 0
Bình luận (0)
Bài 1: Cho hình thang ABCD(AB//CD). Tia phân giác của góc A và góc D cắt nhau tại I, của góc B và góc C cắt nhau tại k. Gọi M,N lần lượt là trung điểm của AD và BC. Cm: 4 điểm M,N,I,K thẳng hàng
Bài 2: Cho hình thang cân ABCD, đáy nhỏ AB. Vẽ AH vuông góc CD. CMR: DH=CD-AB/2
NHANH NHA MÌNH CẦN GẤP LẮM
Cho hình thang ABCD(AB//CD,AB<CD) Gọi M,N,P,Q theo thứ tự là trung điểm của AB,BD,AC,CD. Đường thẳng vuông dóc với MN tại N và đường thẳng vuông góc với MP tại p cắt nhau tại E.
a. CM: tứ giác MNQP là hình bình hành.
b. Gọi I,K lần lượt là trung điểm của AD,BC. CM: NP//DC.
c. CM:ED=EC
GIÚP MÌNH ĐI! GẤP LĂM! SÁNG 9/12/2018 LÀ MÌNH PHẢI NỘP RỒI.
Đúng 0
Bình luận (0)
a) MN là dường trung bình tam giác ABD,PE là đường trung bình tam giác ACD=>MN//AD,PQ//AD=>PE//MN.
tương tự, ta có: NQ//MP. ==>MNQP laf hbh.
b) IP là đường trung bình tam giác ADC=>IP //CD, KN là đường trung bình tam giác BDC=>KN //CD, IK là đường trung bình hình thang ABCD=>IK //CD .==>NP // CD(theo tiên đề ơ-clit).
còn câu c bạn cố gắng nha, khuya quá mẹ mk bắt ngủ nên ko ghi rõ ra, phần đường trung bình là do có các trung điểm đã cho. thông cảm nha
Đúng 0
Bình luận (0)
Cho hình thang ABCD vuông tại A và B có D = 45o, BC = 6cm, AB = 8cm.
a) Tính AD, CD.
b) Gọi M, N, E, F là trung điểm của AB, CD, BD, AC. Chứng minh M, N, E, F thẳng hàng.
c) BN cắt AD tại K, EN cắt CK tại Q. Chứng minh BCKD là hình bình hành, QB = QA.
d) Chứng minh: CK^2 = AC^2 + AK^2 - 2.AC.AK.cosKAC
Em làm được a,b rồi ạ. Mong anh chị giúp em câu c,d ạ.
c.
K thuộc AD nên BC song song DK
Áp dụng định lý Talet: \(\dfrac{BN}{KN}=\dfrac{CN}{DN}=1\Rightarrow BN=KN\) hay N là trung điểm BK
\(\Rightarrow\) BCKD là hình bình hành (tứ giác có 2 đường chéo cắt nhau tại trung điểm mỗi đường)
Theo câu b, E, M, N thẳng hàng nên Q nằm trên MN (1)
Mà MN là đường trung bình của hình thang ABCD
\(\Rightarrow MN||AD\Rightarrow MN\perp AB\) (2)
Mà M là trung điểm AB (3)
(2);(3) \(\Rightarrow\) MN là trung trực AB (4)
(1);(4) \(\Rightarrow QB=QA\)
d.
Hạ CH vuông góc AD
Trong tam giác vuông CHK: \(cosKAC=\dfrac{AH}{AC}\Rightarrow AH=AC.cos\widehat{KAC}\)
Pitago: \(CH^2+AH^2=AC^2\)
Do đó: \(CK^2=CH^2+HK^2=CH^2+\left(AK-AH\right)^2=CH^2+AH^2+AK^2-2AK.AH\)
\(=AC^2+AK^2-2AK.AC.cos\widehat{KAC}\) (đpcm)
Đúng 2
Bình luận (0)
giúp mình với ạ :)
Cho hình thang ABCD (AB//CD), AC cắt BD tại O, AD cắt BC tại I:
a. Cm: OA=OB ; 0C=OD
B. Cm: IC=ID
c. Gọi M là trung điểm AB, N là trung điểm CD. Cmr: I, M, O, N thẳng hàng. \(\)