Cho phương trình:x2-m2x+2m+2=0. Tìm m\(\in\)Z+ để phương trình có nghiệm nguyên

Những câu hỏi liên quan
cho phương trình:
x2 + (2m + 1)x +m2 - 3m = 0 (1)
a) giải phương trình khi x = 1
b) tìm m để phương trình có nghiệm.
a) Thay \(x=1\) vào phương trình, ta được:
\(1+2m+1+m^2-3m=0\) \(\Rightarrow m\in\varnothing\)
Vậy khi \(x=1\) thì phương trình vô nghiệm
b) Xét phương trình, ta có: \(\Delta=16m+1\)
Để phương trình có nghiệm \(\Leftrightarrow\Delta\ge0\) \(\Leftrightarrow m\ge-\dfrac{1}{16}\)
Vậy \(m\ge-\dfrac{1}{16}\)
Đúng 1
Bình luận (0)
Cho phương trình:x2-2(m-1)x+m2-2m=0 (m là tham số)
a,Giải phương trình với m=3
b,Tìm m để phương trình có 1 nghiệm x=-2.Với m tìm được hãy tìm nghiệm còn lại của phương trình
c,Tìm m để phương trình có 2 nghiệm x1 và x2 thỏa mãn:x12+x22=4
a: Thay m=3 vào pt, ta được:
\(x^2-2\cdot\left(3-1\right)x+3^2-2\cdot3=0\)
\(\Leftrightarrow x^2-4x+3=0\)
=>(x-1)(x-3)=0
=>x=1 hoặc x=3
b: \(\text{Δ}=\left[-2\left(m-1\right)\right]^2-4\left(m^2-2m\right)\)
\(=\left(2m-2\right)^2-4\left(m^2-2m\right)\)
\(=4m^2-8m+4-4m^2+8m=4>0\)
Do đó: Phương trình luôn có hai nghiệm phân biệt
Thay x=-2 vào pt, ta được:
\(\left(-2\right)^2-2\cdot\left(-2\right)\cdot\left(m-1\right)+m^2-2m=0\)
\(\Leftrightarrow m^2-2m+4+4\left(m-1\right)=0\)
\(\Leftrightarrow m^2-2m+4+4m-4=0\)
=>m(m+2)=0
=>m=0 hoặc m=-2
Theo hệ thức Vi-et, ta được:
\(x_1+x_2=2\left(m-1\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}x_2-2=2\cdot\left(-1\right)=-2\\x_2-2=2\cdot\left(-3\right)=-6\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x_2=0\\x_2=-4\end{matrix}\right.\)
c: \(x_1^2+x_2^2=4\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=4\)
\(\Leftrightarrow\left(2m-2\right)^2-2\left(m^2-2m\right)=4\)
\(\Leftrightarrow4m^2-8m+4-2m^2+4m-4=0\)
\(\Leftrightarrow2m^2-4m=0\)
=>2m(m-2)=0
=>m=0 hoặc m=2
Đúng 3
Bình luận (1)
cho phương trình:x2-2m.(m-2).x+2m-5=0
a)chứng minh phương trình luôn có 2 nghiệm phân biệt ∀
b) tìm m để có nghiệm phương trình nhỏ hơn 1
c)tìm m để phương trình có 2 nghiệmx1;x2 thỏa mãn x1 -3x2=m
cho phương trình:x2-2m.(m-2).x+2m-5=0
a)chứng minh phương trình luôn có 2 nghiệm phân biệt ∀
b) tìm m để có nghiệm phương trình nhỏ hơn 1
c)tìm m để phương trình có 2 nghiệmx1;x2 thỏa mãn x1 -3x2=m
Cho phương trình: x^2 - m^2x + 2m + 2 = 0. Tìm m ∈ Z để phương trình có nghiệm nguyên
Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn
−
15
;
5
để phương trình
4
x
+
m
2
x
+
2
m
−
4
0
có nghiệm? A. 18. B. 17. C. 20. D. 19.
Đọc tiếp
Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn − 15 ; 5 để phương trình 4 x + m 2 x + 2 m − 4 = 0 có nghiệm?
A. 18.
B. 17.
C. 20.
D. 19.

+) Phương trình ban đầu có nghiệm khi và chỉ khi phương trình bậc hai ẩn t có nghiệm dương.
Cách giải:

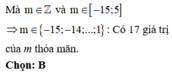
Đúng 0
Bình luận (0)
cho phương trình:
mx - 3 = 2x =2m
1) tìm m để phương trình vô nghiệm, phương trình có nghiệm
2) khi phương trình có nghiệm duy nhất :
a) tìm m nguyên để phương trình có nghiệm nguyên
b) tìm m để phương trình có nghiệm x>0
c) tìm m để phương trình có nghiệm x<0
cho phương trình:
x2 - x - m2 + 3m - 2 = 0 (m là tham số)
tìm m để phương trình có một nghiệm x=7+\(\sqrt{2022}\)
các bạn giúp mình với ạ mình cảm ơn
Thay x=7+căn 2022 vào pt, ta được:
\(49+14\sqrt{2022}+2022-7-\sqrt{2022}+3m-2=0\)
=>\(3m+2062+13\sqrt{2022}=0\)
=.\(m=\dfrac{-2062-13\sqrt{2022}}{3}\)
Đúng 0
Bình luận (0)
Câu 1: Cho hai đường thẳng (d):y=mx+1 và (d'):y=m2x +m+1, trong đó m là tham số. Tìm m để (d) và (d') song song với nhau
Câu 2: Cho phương trình: x2-2mx+m2+2m+2=0 (m là tham số). Tìm m để phương trình đã cho có 2 nghiệm phân biệt x1, x2 thỏa mãn \(\dfrac{2}{x_1}+\dfrac{2}{x_2}=x_1+x_2\)

















