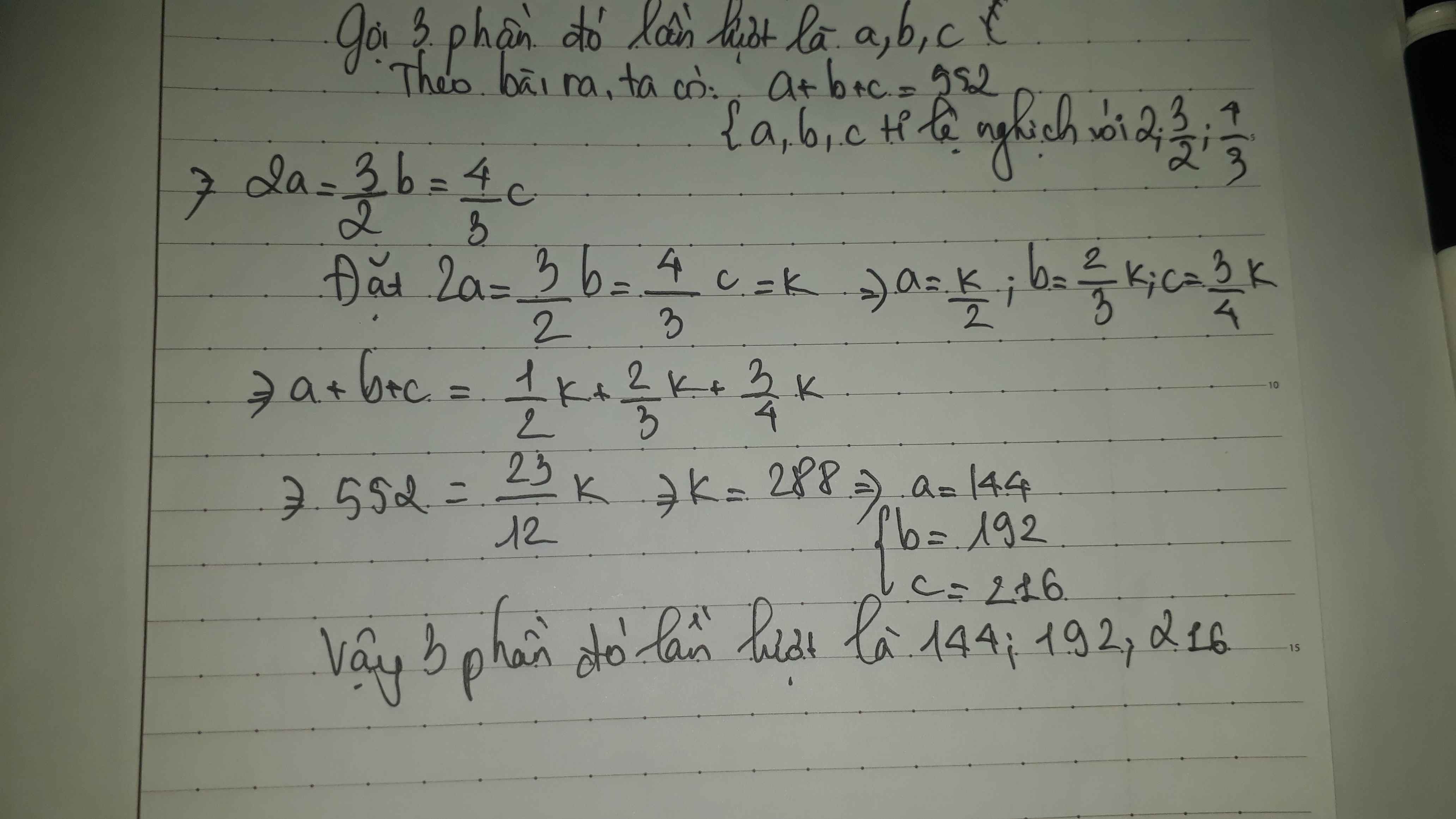Chia số 552 thành 3 phần tỉ lệ thuận với \(\frac{1}{2};\frac{2}{3};\frac{3}{4}\)

Những câu hỏi liên quan
chia số 552 thành 3 phần tỉ lệ thuận với 1/2, 2/3, 3/4
chia số 552 thành 3 phần. biết tỉ lệ thuận với 1 phần 2 / 2 phần 3 / 3 phần 4
a) chia số 552 thành 3 phần tỉ lệ thuận với 3;4;5
b) chia số 315 thành 3 phần tỉ lệ nghịch với 3;4;6
a) gọi 3 phần đó là x, y, z
ta có:
x/3 = y/4 = z/5 và x + y + z = 552
áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
x/3 = y/4 = z/5 = (x + y + z) / (3 + 4 + 5) = 552 / 12 = 46
x/3 = 46 => x = 46 x 3 = 138
y/4 = 46 => y = 46 x 4 = 184
z/5 = 46 => z = 46 x 5 = 230
vậy 3 phần đó là: 138; 184; 230
b) gọi 2 phần đó là a, b, c
ta có:
\(\frac{a}{\frac{1}{3}}=\frac{b}{\frac{1}{4}}=\frac{c}{\frac{1}{6}}\) và a + b + c = 315
áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\frac{a}{\frac{1}{3}}=\frac{b}{\frac{1}{4}}=\frac{c}{\frac{1}{6}}=\frac{a+b+c}{\frac{1}{3}+\frac{1}{4}+\frac{1}{6}}=\frac{315}{\frac{3}{4}}=420\)
\(\frac{a}{\frac{1}{3}}=420\Rightarrow a=420\cdot\frac{1}{3}=140\)
\(\frac{b}{\frac{1}{4}}=420\Rightarrow b=420\cdot\frac{1}{4}=105\)
\(\frac{c}{\frac{1}{6}}=420\Rightarrow c=420\cdot\frac{1}{6}=70\)
vậy 3 phần đó là:140, 105, 70
Đúng 0
Bình luận (0)
I. Nội qui tham gia "Giúp tôi giải toán"
1. Không đưa câu hỏi linh tinh lên diễn đàn, chỉ đưa các bài mà mình không giải được hoặc các câu hỏi hay lên diễn đàn;
2. Không trả lời linh tinh, không phù hợp với nội dung câu hỏi trên diễn đàn.
3. Không "Đúng" vào các câu trả lời linh tinh nhằm gian lận điểm hỏi đáp.
Các bạn vi phạm 3 điều trên sẽ bị giáo viên của Online Math trừ hết điểm hỏi đáp, có thể bị khóa tài khoản hoặc bị cấm vĩnh viễn không đăng nhập vào trang web.
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
a) chia số 552 thành 3 phần tỉ lệ thuận với 3,4,5
b) chia số 315 thành 3 phần tỉ lệ nghịch vs 3,4,6
a) gọi 3 phần đó là x, y, z
ta có:
x/3 = y/4 = z/5 và x + y + z = 552
áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
x/3 = y/4 = z/5 = (x + y + z) / (3 + 4 + 5) = 552 / 12 = 46
x/3 = 46 => x = 46 x 3 = 138
y/4 = 46 => y = 46 x 4 = 184
z/5 = 46 => z = 46 x 5 = 230
vậy 3 phần đó là: 138; 184; 230
b) gọi 2 phần đó là a, b, c
ta có:
a phần 1/3=b phần 1/4=c phần 1/6 và a + b + c = 315
áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
a phần 1/3=b phần 1/4=c / 1/6=a+b+c phần 1/3+1/4+1/6=315 phần 3/4=420
a phần 1/3=420⇒a=140
b phần 1/4=420⇒b=105
c phần 1/6=420⇒c=70
vậy............
đây là toán nâng cao lớp 7 đúng ko
giúp mik vs ạ !
a) chia số 552 thành 3 phần tỷ lệ thuận với 3; 4; 5
b) chia số 315 thành 3 phần tỉ lệ nghịch với 3;5;6
a: Áp dụng tính chất của dãy tỉ số bằng nhau, ta đc:
\(\dfrac{a}{3}=\dfrac{b}{4}=\dfrac{c}{5}=\dfrac{a+b+c}{3+4+5}=\dfrac{552}{12}=46\)
=>a=138; b=184; c=230
b: Gọi ba số cần tìm lần lượt là a,b,c
Theo đề, ta có: 3a=5b=6c
=>a/10=b/6=c/5
Áp dụng tính chất của DTSBN, ta đc:
\(\dfrac{a}{10}=\dfrac{b}{6}=\dfrac{c}{5}=\dfrac{a+b+c}{10+6+5}=\dfrac{315}{21}=15\)
=>a=150; b=90; c=75
Đúng 0
Bình luận (0)
Câu 1: a) Chia số 552 thành 3 phần tỉ lệ thuận với 3; 4; 5.
b) Chia số 315 thành 3 phần tỉ lệ nghịch với 3; 4; 6.
Câu 2: Tìm các số hữu tỉ x, y, z biết rằng: \(\frac{x}{11}=\frac{y}{12};\frac{y}{3}=\frac{z}{7}\) và 2x - y + z = 512.
#)Trả lời :
Câu 1 :
a) Gọi ba phần đó là a, b, c
Theo đầu bài, ta có : a, b, c tỉ lệ thuận với 3; 4; 5 => \(\frac{a}{3}=\frac{b}{4}=\frac{c}{5}\)và a + b + c = 552
Áp dụng tính chất dãy tỉ số bằng nhau ( đến đây bn tự lm típ hen )
b) Gọi ba phần đó là a, b, c
Theo đầu bài, ta có : a, b, c tỉ lệ nghịch với 3, 4, 6 => a, b, c tỉ lệ nghịch với \(\frac{1}{3};\frac{1}{4};\frac{1}{6}\)
=> \(\frac{a}{\frac{1}{3}}=\frac{b}{\frac{1}{4}}=\frac{c}{\frac{1}{6}}\)và a + b + c = 315
Áp dụng tính chất dãy tỉ số bằng nhau ( đến đây tự lm típ hen :D )
Câu 2 :
\(\frac{x}{11}=\frac{y}{12}\Rightarrow\frac{2x}{22}=\frac{y}{12}\left(1\right)\)
\(\frac{y}{3}=\frac{z}{7}\Rightarrow\frac{y}{12}=\frac{z}{28}\left(2\right)\)
Từ (1) và (2) suy ra \(\frac{2x}{22}=\frac{y}{12}=\frac{z}{28}\)
Áp dụng tính chất dãy tỉ số bằng nhau :
\(\frac{2x}{22}=\frac{y}{12}=\frac{z}{28}=\frac{2x-y+z}{22-12+28}=\frac{152}{38}\)
\(\Rightarrow x=44;y=48;z=112\)
#~Will~be~Pens~#
Đúng 0
Bình luận (0)
1a) Gọi ba phần đó là x, y, z.
Vì x, y, z tỉ lệ với 3, 4, 5 nên \(\frac{x}{3}=\frac{y}{4}=\frac{z}{5}\)
Áp dụng tính chất của dãy các tỉ số bằng nhau, ta có:
\(\frac{x}{3}=\frac{y}{4}=\frac{z}{5}=\frac{x+y+z}{3+4+5}=\frac{552}{12}=46\)
\(\Rightarrow\hept{\begin{cases}x=46.3=138\\y=46.4=184\\z=46.5=230\end{cases}}\)
Vậy 3 phần đó là 138, 184, 230
Đúng 0
Bình luận (0)
b) Gọi 3 phần đó là a, b, c .
Ta có: a, b, c tỉ lệ nghịch với 3, 4, 6 nên \(\frac{a}{\frac{1}{3}}=\frac{b}{\frac{1}{4}}=\frac{c}{\frac{1}{6}}\)
Áp dụng tính chất của dãy các tỉ số bằng nhau, ta có:
\(\frac{a}{\frac{1}{3}}=\frac{b}{\frac{1}{4}}=\frac{c}{\frac{1}{6}}=\frac{a+b+c}{\frac{1}{3}+\frac{1}{4}+\frac{1}{6}}=\frac{315}{\frac{3}{4}}=420\)
\(\Rightarrow\hept{\begin{cases}a=420.\frac{1}{3}=140\\b=420.\frac{1}{4}=105\\c=420.\frac{1}{6}=70\end{cases}}\)
Vậy 3 phần đó lần lượt là 140, 105, 70
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Chia số 552 thành ba phần tỉ lệ thuận với 3; 4; 5
Gọi x, y, z là ba số cần tìm
Do x, y, z tỉ lệ thuận với 3; 4; 5 nên:
x/3 = y/4 = c/5
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
x/3 = y/4 = c/5 = (a + b + c)/(3 + 4 + 5) = 552/12 = 46
x/3 = 46 ⇒ x = 46.3 = 138
y/4 = 46 ⇒ y = 46.4 = 184
z/5 = 46 ⇒ z = 46.5 = 230
Vậy ba số cần tìm là 138; 184; 230
Đúng 1
Bình luận (0)
chia số 552 thành 3 phần tỉ lệ nghịch với 2; \(\dfrac{3}{2}\); \(\dfrac{4}{3}\)
tìm 3 phần đó
a)Tìm ba số a,b,c biết rằng chúng tỉ lệ thuận với 3,5,7 và b-a=10
b)Chia số 552 thành 3 phần tỉ lệ thuận với 3,4,5
a)Tìm ba số a,b,c biết rằng chúng tỉ lệ thuận với 3,5,7 và b-a=10
ba số a,b,c tỉ lệ thuận với 3,5,7
\(\Rightarrow\dfrac{a}{3}=\dfrac{b}{5}=\dfrac{c}{7}\)
Áp dụng tính chất của dãy tỉ số bằng nhau ,ta có :
\(\dfrac{a}{3}=\dfrac{b}{5}=\dfrac{c}{7}=\dfrac{b-a}{5-3}=\dfrac{10}{2}=5\) \(\Rightarrow\left\{{}\begin{matrix}\dfrac{a}{3}=5\Rightarrow a=15\\\dfrac{b}{5}=5\Rightarrow b=25\\\dfrac{c}{7}=5\Rightarrow c=35\end{matrix}\right.\) Vậy \(a=15;b=25;c=35\)b)Chia số 552 thành 3 phần tỉ lệ thuận với 3,4,5
Gỉa sử chia số 552 thành tổng ba số a,b,c
\(\Rightarrow a+b+c=552\)
Vì ba số tỉ lệ thuận với 3,4,5
\(\Rightarrow\dfrac{a}{3}=\dfrac{b}{4}=\dfrac{c}{5}\)
Áp dụng tính chất của dãy tỉ số bằng nhau ,ta có :
\(\dfrac{a}{3}=\dfrac{b}{4}=\dfrac{c}{5}=\dfrac{a+b+c}{3+4+5}=\dfrac{552}{12}=46\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{a}{3}=46\Rightarrow a=138\\\dfrac{b}{4}=46\Rightarrow b=184\\\dfrac{c}{5}=46\Rightarrow c=230\end{matrix}\right.\)
Vậy \(a=138;b=184;c=230\)
Đúng 0
Bình luận (0)