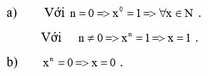Cho a,b,n ∈ N*. Biết rằng với mọi số tự nhiên k khác b ta đều có kn - a ⋮ k - b

Những câu hỏi liên quan
Cho a, b, n là các số nguyên dương. Biết rằng với mọi số tự nhiên k khác b ta đều có k^n - a chia hết cho k - b. CMR: a = b^n
B1:chứng minh rằng với mọi số tự nhiên(n>hoặc =2) luôn tìm được n số tự nhiên liên tiếp đồng thời là hợp số.
B2:Cho a= 50!=1.2.3........50 Chứng tỏ rằng 49 số tự nhiên sau đều là hợp số: a+2;a+3;a+4;.........;a+50
B3:Tìm k thuộc N,sao cho: a,7.k là số nguyên tố b,k;k+6;k+8;k+12;k+14 đề là số nguyên tố
Giúp mình nhanh với
B1:chứng minh rằng với mọi số tự nhiên(n>hoặc =2) luôn tìm được n số tự nhiên liên tiếp đồng thời là hợp số.
B2:Cho a= 50!=1.2.3........50
Chứng tỏ rằng 49 số tự nhiên sau đều là hợp số:
a+2;a+3;a+4;.........;a+50
B3:Tìm k thuộc N,sao cho:
a,7.k là số nguyên tố
b,k;k+6;k+8;k+12;k+14 đề là số nguyên tố
A. Tìm số tự nhiên a, biết rằng với mọi n ϵ N ta có an = 1
B. Tìm số tự nhiên x mà x50 = x
a: a^n=1
=>a^n=1^n
=>a=1
b: x^50=x
=>x^50-x=0
=>x(x^49-1)=0
=>x=0 hoặc x^49-1=0
=>x=0 hoặc x^49=1
=>x=0 hoặc x=1
Đúng 0
Bình luận (0)
Cho a,b,n ∈ N*. Biết rằng với mọi số tự nhiên k khác b ta đều có kn - a ⋮ k - b. Chứng minh rằng a=bn
Akai Haruma, Nguyễn Việt Lâm, Y, svtkvtm please help me!!!
svtkvtm bài giải đây nha
Xét k > b
Ta có:
\(\left\{{}\begin{matrix}k^n-a⋮k-b\\k^n-b^n⋮k-b\end{matrix}\right.\)
\(\Rightarrow b^n-a⋮k-b\)
Mà theo đề bài là với mọi k khác b nên sẽ tồn tại số k sao cho
\(\left\{{}\begin{matrix}k-b>b^n-a\left(b^n-a>0\right)\\k-b< b^n-a\left(b^n-a< 0\right)\end{matrix}\right.\)
Điều này chỉ xảy ra khi \(b^n-a=0\)hay \(a=b^n\)
Đúng 0
Bình luận (2)
Ý quên xóa dòng xét k > b dòng này bỏ nha.
Đúng 0
Bình luận (0)
Tìm số tự nhiên x, biết rằng với mọi n ∈ N ta có:
a) x n = 1
b) x n = 0
Tìm số tự nhiên x, biết rằng với mọi n ∈ N ta có:
a, x n = 1
b, x n = 0
a, Với n = 0 => x 0 = 1 ⇒ ∀ x ∈ N
Với n ≠ 0 => x n = 1 ⇒ x = 1
b, x n = 0 => x = 0
Đúng 0
Bình luận (0)
a,Chứng minh rằng với mọi số tự nhiên n khác 0 ta luôn có:
1²+2²+3²+...+n²=n.(n+1).(2n+1)/6
b,Chứng minh rằng
A=1.5+2.6+3.7+...+2023.2027
chia hết các số 11;23 và 2023
c,Tìm tất cả các số tự nhiên n (1 ≤ n ≤ 2000) để biểu thức B=1.3+2.3+...+n.(n+2) chia hết cho 2027