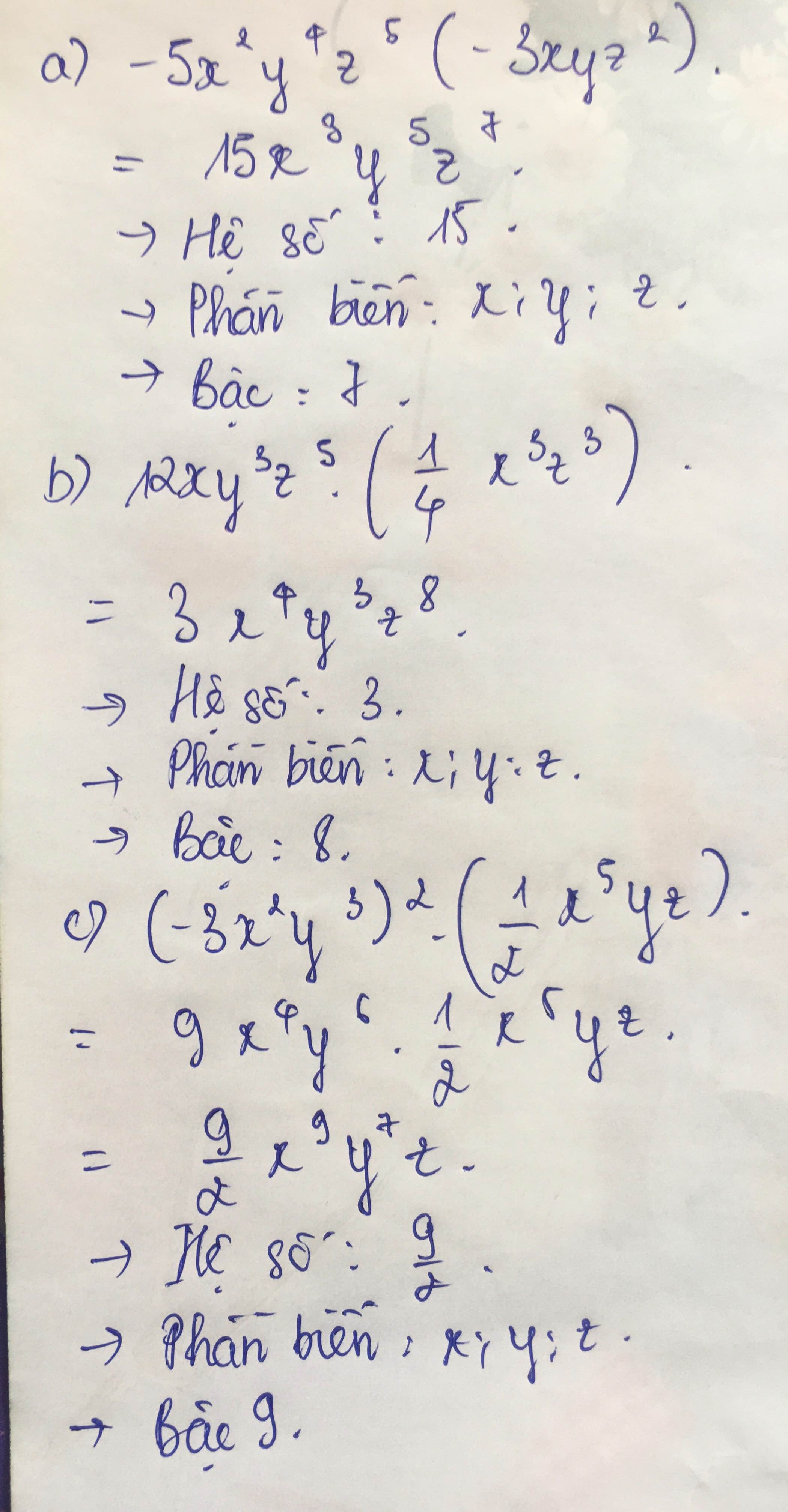Dễ mà nhân ra ik r` bt

a) \(M\left(x\right)=-2x^5+5x^2+7x^4-5x+8+2x^5-7x^4-4x^2+6\)

\(=\left(-2x^5+2x^5\right)+\left(7x^4-7x^4\right)+\left(5x^2-4x^2\right)-9x+\left(8+6\right)\)

\(=x^2-9x+14\)

\(N\left(x\right)=7x^7+x^6-5x^3+2x^2-7x^7+5x^3+3\)

\(=\left(7x^7-7x^7\right)+x^6-\left(5x^3-5x^3\right)+2x^2+3\)

\(=x^6+2x^2+3\)

b) Đa thức M(x) có hệ số cao nhất là 1 

                                hệ số tự do là 14

                                bậc 2

 Đa thức N(x) có hệ số cao nhất là 1 

                            hệ số tự do là 3 

                            bậc 6

\(a.=15x^3y^5z^7\) có hệ số là 15 ; phần biến là:x³y⁵z⁷ ; bậc là:15

b.\(=3x^4y^3z^8\)có hệ số là: 3 ;phần biến là: x⁴y³z⁸ ;có bậc là:15

\(\left(x-3x\right)^3=\left(-2x\right)^3=-8x^3\)

Hệ số của hạng tử bậc là 3 là -8

\(\left(x^{-4}+x^{\frac{5}{2}}\right)^{12}\) có SHTQ: \(C_{12}^kx^{-4k}.x^{\frac{5}{2}\left(12-k\right)}=C^k_{12}x^{30-\frac{13}{2}k}\)

Số hạng chứa \(x^8\Rightarrow30-\frac{13}{2}k=8\Rightarrow\) ko có k nguyên thỏa mãn

Vậy trong khai triển trên ko có số hạng chứa \(x^8\)

b/ \(\left(1-x^2+x^4\right)^{16}\)

\(\left\{{}\begin{matrix}k_0+k_2+k_4=16\\2k_2+4k_4=16\end{matrix}\right.\)

\(\Rightarrow\left(k_0;k_2;k_4\right)=\left(8;8;0\right);\left(9;6;1\right);\left(10;4;2\right);\left(11;2;3\right);\left(12;0;4\right)\)

Hệ số của số hạng chứa \(x^{16}\):

\(\frac{16!}{8!.8!}+\frac{16!}{9!.6!}+\frac{16!}{10!.4!.2!}+\frac{16!}{11!.2!.3!}+\frac{16!}{12!.4!}=...\)

c/ SHTQ của khai triển \(\left(1-2x\right)^5\) là \(C_5^k\left(-2\right)^kx^k\)

Số hạng chứa \(x^4\) có hệ số: \(C_5^4.\left(-2\right)^4\)

SHTQ của khai triển \(\left(1+3x\right)^{10}\) là: \(C_{10}^k3^kx^k\)

Số hạng chứa \(x^3\) có hệ số \(C_{10}^33^3\)

\(\Rightarrow\) Hệ số của số hạng chứa \(x^5\) là: \(C_5^4\left(-2\right)^4+C_{10}^3.3^3\)

 \(A=\left(2x+1\right)\left(x+1\right)^2\left(2x+3\right)-18\)

\(=\frac{1}{4}\left[\left(2x+1\right)\left(x+1\right)^2.4\left(2x+3\right)\right]-72\)

\(=\frac{1}{4}\left[\left(2x+1\right)\left(2x+3\right)\left(2x+2\right)^2\right]-72\)

\(=\frac{1}{4}\left[\left(4x^2+8x+3\right)\left(4x^2+8x+4\right)-72\right]\)

Đặt: \(4x^2+8x+3=t\)

Ta có:  \(A=\frac{1}{4}\left[t^2+t-72\right]\)

\(=\frac{1}{4}\left[\left(t+9\right)\left(t-8\right)\right]\)

\(=\frac{1}{4}\left[\left(4x^2+8x+12\right)\left(4x^2+8x-5\right)\right]\)

\(=\left(x^2+2x+3\right)\left[4x^2+8x-5\right]\)

\(=\left(x^2+2x+3\right)\left(2x-1\right)\left(2x+5\right)\)

 \(B=\left(4x+1\right)\left(12x-1\right)\left(3x+2\right)\left(x+1\right)-4\)

\(=\left[\left(4x+1\right)\left(3x+2\right)\right]\left[\left(12x-1\right)\left(x+1\right)\right]-4\)

\(=\left(12x^2+11x+2\right)\left(12x^2+11x-1\right)-4\)

Đặt \(12x^2+11x+2=a\)

Khi đó: \(B=a\left(a-3\right)-4\)

\(=a^2-3a-4=\left(a+1\right)\left(a-4\right)\)

\(=\left(12x^2+11x+3\right)\left(12x^2+11x-2\right)\)

        \(\left(x^2-x+2\right)^2+\left(x-2\right)^2\)

\(=x^4+x^2+4-2x^3-4x+4x^2+x^2-4x+4\)

\(=x^4-2x^3+6x^2-8x+8\)

\(=x^4-2x^3+2x^2+4x^2-8x+8\)

\(=x^2\left(x^2-2x+2\right)+4\left(x^2-2x+2\right)=\left(x^2-2x+2\right)\left(x^2+4\right)\)

       \(3x^4-5x^3-18x^2-3x+5\)

\(=3x^4+x^3-x^2-6x^3-2x^2+2x-15x^2-5x+5\)

\(=x^2\left(3x^2+x-1\right)-2x\left(3x^2+x-1\right)-5\left(3x^2+x-1\right)\)

\(=\left(3x^2+x-1\right)\left(x^2-2x-5\right)\)

Bài này thật sự khó và hay đấy.

a/ \(\frac{A^4_n}{A_{n+1}^3-C_n^{n-4}}=\frac{24}{23}\Rightarrow n=5\)

Khai triển \(\left(2-3x^2+x^3\right)^5\)

\(\left\{{}\begin{matrix}k_0+k_2+k_3=5\\2k_2+3k_3=9\end{matrix}\right.\) \(\Rightarrow\left(k_0;k_2;k_3\right)=\left(1;3;1\right);\left(2;0;3\right)\)

Hệ số của số hạng chứa \(x^9\):

\(\frac{5!}{1!.3!.1!}.2^1.\left(-3\right)^3+\frac{5!}{2!.3!}.2^2.\left(-3\right)^0=-1040\)

b/ SHTQ của khai triển: \(\left(1+2x\right)^n\) là: \(C_n^k2^kx^k\)

\(\Rightarrow\) Hệ số của \(x^3\) trong khai triển tổng quát là \(C_n^32^3\)

\(\Rightarrow\) Hệ số của \(x^3\) trong khai triển của \(f\left(x\right)\): \(2^3.\sum\limits^{22}_{n=3}C_n^3\)

Tính tổng \(C_3^3+C_4^3+C_5^3+...+C_{22}^3\)

\(=C_4^4+C_4^3+C_5^3+...+C_{22}^3\)

\(=C_5^4+C_5^3+...+C_{22}^3\)

\(=C_6^4+C_6^3+...+C_{22}^3=...=C_{23}^4\)

Vậy \(2^3\sum\limits^{22}_{n=3}C_n^3=2^3.C_{23}^4\)

1) \(A\left(x\right)=-5x^3+3x^4+\frac{5}{7}-8x^2-10x\)

\(A\left(x\right)=3x^4-5x^3-8x^2-10x+\frac{5}{7}\)

\(B\left(x\right)=-2x^4-\frac{2}{7}+7x^2+8x^3+6x\)

\(B\left(x\right)=-2x^4+8x^3+7x^2+6x-\frac{2}{7}\)

2)       \(A\left(x\right)=3x^4-5x^3-8x^2-10x+\frac{5}{7}\)

      +

          \(B\left(x\right)=-2x^4+8x^3+7x^2+6x-\frac{2}{7}\)

\(A\left(x\right)+B\left(x\right)=x^4+3x^3-x^2-4x+\frac{3}{7}\)

                \(A\left(x\right)=3x^4-5x^3-8x^2-10x+\frac{5}{7}\)

-

                \(B\left(x\right)=-2x^4+8x^3+7x^2+6x-\frac{2}{7}\)

\(A\left(x\right)-B\left(x\right)=5x^4-13x^3-15x^2-16x+1\)