Ta có AB^2+AC^2=10^2+24^2=676

      BC^2=26^2=676

=> Tam Giác ABC vuông tại A(đpcm)

b, \(\sin B=\frac{AC}{BC}=\frac{24}{26}=\frac{12}{13}\)

\(\sin C=\frac{AB}{BC}=\frac{10}{26}=\frac{5}{13}\)

c,Áp dụng hệ thức   AB.AC=AH.BC

           => AH=AB.AC/BC=10.24/26=9,2

\(AB^2=BH.BC\)\(\Leftrightarrow10^2=BH.26\)\(\Rightarrow BH\approx3,8\)

\(\Rightarrow CH=22,2\)

- cảm ơn ạ 

a,theo định lý pytago đảo tính dc A=90

các góc còn lại tính bằng máy tính nha bạn.bạn lấy máy tính bấm \(sin^{-1}\)(cạnh đối/cạnh huyền) là ra góc cần tính nha bạn

b,ah vuông góc bc mà tam giác abc vuông tại a nên

   \(AB^2=BH.BC\Rightarrow100=BH.26\Rightarrow BH=\dfrac{50}{13}\)

   \(\Rightarrow CH=BC-BH=\dfrac{288}{13}\)

\(\Rightarrow AH^2=BH.CH=\dfrac{14400}{169}\Rightarrow AH=\dfrac{120}{13}\)

tick mik nha bn

.

a,
xét tam giác BAC và tam giác BHA có
góc B chung
góc BAC=góc BHA (=90 độ)
=>tam giác BAC đông dạng với tam giác BHA
ta có \(\dfrac{AB}{BH}=\dfrac{BC}{BA}\)=>\(AB^2=BH.BC\)
b,
Xét Tam giác ABC 
=>\(\dfrac{AB}{AH}=\dfrac{BC}{AC}\)=>AB.AC=AH.BC
c,
áp dụng định lý py-ta-go vào tam giác ABC vuông tại A
\(AC^2=BC^2-BA^2\)
=>AC=8
Xét tam giác ABC 
\(\dfrac{AC}{CH}=\dfrac{AB}{BH}=>\dfrac{8}{CH}=\dfrac{6}{10-CH}\)
=>8(10-CH)=6CH
=>80-8CH=6CH
=>CH sấp sỉ 5cm
áp dụng định lý py-ta-go vào tam giác HBA vuuong tại H
\(AH^2=AB^2-BH^2\)
=>AH=3,31662479

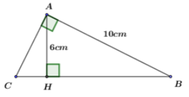
Áp dụng định lý Pytago trong tam giác ABH vuông tại H. Ta có:

Trong tam giác vuông ABC vuông tại A có AH là đường cao

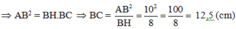
Áp dụng định lý Py-ta-go cho tam giác vuông ABC ta có:

Vậy AC = 7,5 (cm); BC =  12,5 (cm)

Đáp án cần chọn là: B

a: ΔABC vuông tại A

=>\(AB^2+AC^2=BC^2\)

=>\(AC^2=10^2-6^2=64\)

=>AC=8(cm)

Xét ΔABC vuông tại A có AH là đường cao

nên \(\left\{{}\begin{matrix}AH\cdot BC=AB\cdot AC\\AB^2=BH\cdot BC\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}AH=\dfrac{6\cdot8}{10}=4,8\left(cm\right)\\BH=\dfrac{6^2}{10}=3,6\left(cm\right)\end{matrix}\right.\)

b: ΔAHB vuông tại H có HE là đường cao

nên \(AE\cdot AB=AH^2\left(1\right)\)

ΔAHC vuông tại H có HF là đường cao

nên \(AF\cdot AC=AH^2\left(2\right)\)

Từ (1) và (2) suy ra AE*AB=AF*AC

=>AE/AC=AF/AB

Xét ΔAEF vuông tại A và ΔACB vuông tại A có

AE/AC=AF/AB

Do đó: ΔAEF đồng dạng với ΔACB

c: Xét ΔBAC có BD là phân giác

nên \(\dfrac{AD}{AB}=\dfrac{CD}{CB}\)

=>\(\dfrac{AB}{AD}=\dfrac{CB}{CD}\)

Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{AB}{AD}=\dfrac{CB}{CD}=\dfrac{AB+BC}{AD+CD}=\dfrac{AB+BC}{AC}\)(1)

ΔBAD vuông tại A có

\(cotABD=\dfrac{AB}{AD}\)(2)

BD là phân giác của góc ABC

=>\(\widehat{ABD}=\widehat{DBC}\left(3\right)\)

Từ (1),(2),(3) suy ra \(cotDBC=\dfrac{AB+BC}{AC}\)

bạn hỏi nhiều quá , các bạn nhìn vào ko biết trả lời sao đâu !!!

rối mắt quá mà viết dày nên bài nọ xọ bài kia mình ko trả lời được cho dù biết rất rõ

viet ba dao nhu the co ma lam dc!!! 

a, Xét ΔHBA và ΔABC có :

\(\widehat{H}=\widehat{A}=90^0\)

\(\widehat{B}:chung\)

\(\Rightarrow\Delta HBA\sim\Delta ABC\left(g-g\right)\)

\(\Rightarrow\dfrac{AB}{BC}=\dfrac{AH}{AC}\)

\(\Rightarrow AB.AC=BC.AH\)

b, Xét ΔABC vuông A, theo định lý Pi-ta-go ta được :

\(\Rightarrow BC=\sqrt{AB^2+AC^2}=\sqrt{12^2+16^2}=20\left(cm\right)\)

Ta có : \(\Delta HBA\sim\Delta ABC\left(cmt\right)\)

\(\Rightarrow\dfrac{AB}{BC}=\dfrac{AH}{AC}\)

hay \(\dfrac{12}{20}=\dfrac{AH}{16}\)

\(\Rightarrow AH=\dfrac{12.16}{20}=9,6\left(cm\right)\)