Cho tam giác ABC cân tại A, điểm D bất kì thuộc cạnh AC. ch/minh DC< DB

Những câu hỏi liên quan
Cho tam giác ABC cân tại A, D là điểm bất kì nằm trong tam giác sao cho góc ADB > góc ADC. Chứng minh DC > DB
Cho tam giác ABC cân tại A. D là một điểm bất kì trong tam giác sao cho góc ADB lớn hơn góc ADC. Chứng minh DC>DB
vì góc ADB > góc ADC
=> DB < DC
Đúng 0
Bình luận (1)
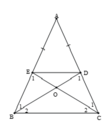
Cho tam giác ABC cân tại A. Lấy điểm D thuộc cạnh AC, lấy điểm E thuộc cạnh AB sao cho AD=AE a) Chứng minh DB=EC b) Gọi O là giao điểm của DB và EC. Chứng minh và là các tam giác cân c) Chứng minh DE / / BC
Cho tam giác ABC cân tại A. Lấy điểm D thuộc cạnh AC, lấy điểm E thuộc cạnh AB sao cho AD=AE
a/Chứng minh DB=EC
b/Gọi O là giao điểm của DB và EC . Chứng minh tam giác OBC và tam giác ODE là các tam giác cân
c/Chứng minh DE // BC
a) Xét △ABD và △ACE có:
AB = AC (gt)
\(\widehat{A}\) chung
AD = AE (gt)
\(\Rightarrow\)△ABD = △ACE (c.g.c)
\(\Rightarrow\)DB = EC (cặp cạnh tương ứng)
b) Ta có :△ABD = △ACE
\(\Rightarrow\widehat{B_1}=\widehat{C_1}\) (cặp góc tương ứng)
Mà \(\widehat{ABC}=\widehat{ACB}\) ( △ABC cân tại đỉnh A)
\(\Rightarrow\widehat{ABC}-\widehat{B_1}=\widehat{ACB}-\widehat{C_1}\)
\(\Rightarrow\widehat{OBC}=\widehat{OCB}\)
\(\Rightarrow\)△OBC cân tại đỉnh O
\(\Rightarrow\)OB = OC
Ta có: DB = EC (cmt)
OB = OC
\(\Rightarrow\)DB - OB = EC - OC
\(\Rightarrow\)OE = OD
\(\Rightarrow\)△ODE cân đỉnh O (ĐPCM)
c) △OBC cân tại đỉnh O
\(\Rightarrow\)\(\widehat{OCB}=\frac{180^o-\widehat{BOC}}{2}\)
△ODE cân tại đỉnh O
\(\Rightarrow\widehat{DEO}=\frac{180^o-\widehat{DOE}}{2}\)
Mà \(\widehat{BOC}=\widehat{DOE}\)(đối đỉnh)
\(\Rightarrow\widehat{DEO}=\widehat{OCB}\)
Vì 2 góc này nằm ở vị trí so le trong
\(\Rightarrow\)DE // BC (ĐPCM)
1. cho tam giác ABC bất kì , có:AB=4cm, AC=6cm, AD là phân giác góc A
a)tính DB/DC
b)tính DC khi DC=3cm
2. cho tam giác ABC vuông tại A, có AB=3cm,AC=4cm.vẽ đường cao AH(H thuộc BC)
a) tính độ dài BC
b) chứng minh tam giác HBA~HAC
c) chứng minh HA2=HB.HC
d) kẻ đường phân giác AD(D THUỘC BC). TÍNH ĐỘ DÀI DB VÀ DC
Cho tam giác ABC vuông cân tại B, có trung tuyến BM. Gọi D là một điểm bất kì thuộc cạnh AC. Kẻ AH, CK vuông góc với BD (H, K thuộc đường thẳng BD). Chứng minh : a) BH = CK. b) Tam giác MHK vuông cân.
xin lỗi tôi ko biết
ai mik lại
ai duyệt mình duyệt lại
ai đúng mình dừng lại
chon a,b,c
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A lấy điểm D thuộc cạnh ac lấy điểm E thuộc cạnh AB Sao cho AD = EC
a,AE chứng minh DB = AC
b,Gọi O là giao điểm của d b và AC Chứng minh tam giác OBC bài tam giác bde là các tam giác cân
C,Chứng minh song song bc
cho tam giác ABC vuông cân tại A, có trung tuyến BM. Gọi D là điểm bất kì thuộc cạnh AC. kẻ AH, CK vuông góc với BD( H,K thuộc BD). Chứng minh:
a) BH=CK
b)tam giác MHK vuông cân
Hình hơi lệch mọi người thông cảm
Đúng 0
Bình luận (0)
cho tam giác ABC cân tại A, H là trung điểm của BC. lấy điểm D thuộc cạnh SB. điểm E thuộc cạnh AC sao cho AD+AE.
a) chứng minh DB=AE
b) chứng minh tam giác BDH= tam giác CEH
điểm D thuộc cạnh AB*
-ghi lộn :"))