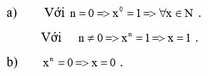Tìm số tự nhiên x biết : 3x1-n(xn+1+yn+1)- 3x1-nyn+1=27

Những câu hỏi liên quan
Tìm P biết
x
−
1
x
2
−
x
+
1
−
P
2
x
−
1
+
3x
1
−
x
3...
Đọc tiếp
Tìm P biết x − 1 x 2 − x + 1 − P = 2 x − 1 + 3x 1 − x 3 .
A. P = x x − 1
B. P = 1 x − 1
C. P = 2 1 - x
D. P = - 1 x - 1
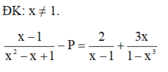
P = x − 1 x 2 − x + 1 − 2 x − 1 − 3 x 1 − x 3 ' P = x − 1 x 2 − x + 1 − 2 x − 1 + 3 x x 3 − 1
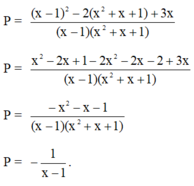
Đáp án cần chọn là: D
Đúng 0
Bình luận (0)
Tìm số tự nhiên x, biết rằng với mọi n ∈ N ta có:
a) x n = 1
b) x n = 0
Tìm số tự nhiên x, biết rằng với mọi n ∈ N ta có:
a, x n = 1
b, x n = 0
a, Với n = 0 => x 0 = 1 ⇒ ∀ x ∈ N
Với n ≠ 0 => x n = 1 ⇒ x = 1
b, x n = 0 => x = 0
Đúng 0
Bình luận (0)
x^2+5x+k=0 có 2 nghiệm x1,x2 thoả mãn 3x1+2x2=1 (Tìm k)
Cho phương trình x2 +2x +m =0 với m là tham số
1) Tìm m để phương trình nhân x = 3 là nghiệm
2) Tìm m để phương trình có hai nghiệm x1, x2 thoả mãn 3x1 +2x2 = 1
1: Thay x=3 vào pt,ta được:
9+6+m=0
hay m=-15
2: \(\text{Δ}=2^2-4\cdot1\cdot m=-4m+4\)
Để phương trình có hai nghiệm thì -4m+4>=0
hay m<=1
Theo đề, ta có hệ phươg trình:
\(\left\{{}\begin{matrix}3x_1+2x_2=1\\x_1+x_2=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_1=5\\x_2=-7\end{matrix}\right.\)
Theo Vi-et,ta được:
\(x_1x_2=m\)
=>m=-35(nhận)
Đúng 0
Bình luận (0)
tìm m để pt x^2+2x+m-1=0 có hai nghiệm x1x2 thỏa mãn 3x1+2x2=2
cho phương trình x^2-(2m+1)x+m-1=0.Tìm m để phương trình có hai nghiệm phân biệt thỏa mãn điều kiện 3x1-4x2=12
Tính:(1-1/2x1/2)x(1-1/3x1/3)x(1-1/4x1/4)x…x(1-1/2007x1/2007)
(1-1/2x1/2)x(1-1/3x1/3)x(1-1/4x1/4)x…x(1-1/2007x1/2007) = ( 1 - 1/4 ) x ( 1 - 1/9 ) x ( 1- 1/16) x .....x ( 1 - 1/4028049) = 3/4 x 8/9 x 15/16 x .....x 4028048 / 4028049 = 3 x 8 x 15 x .....x 4028048 / 4 x 9 x 16 x ......x 4028049 = 1 x 3 x 2 x 4 x 3 x 5 x .....x 2006 x 2008 / 2x2 x 3 x3 x 4 x 4 x .....x 2007 x 2007 = ( 1 x 2 x 3 x .....x 2006) x ( 3 x 4 x 5 x .....x 2008) / ( 2 x 3 x 4 x ....x 2007) x ( 2 x 3 x 4 x ....x 2007) = 2008 / 2007 x 2 = 1004 / 2007
Đúng 0
Bình luận (0)
Tính:
(1-1/2x1/2)x(1-1/3x1/3)x(1-1/4x1/4)x…x(1-1/2007x1/2007)
(1-1/2x1/2)x(1-1/3x1/3)x(1-1/4x1/4)x…x(1-1/2007x1/2007)
= ( 1 - 1/4 ) x ( 1 - 1/9 ) x ( 1- 1/16) x .....x ( 1 - 1/4028049)
= 3/4 x 8/9 x 15/16 x .....x 4028048 / 4028049
= 3 x 8 x 15 x .....x 4028048 / 4 x 9 x 16 x ......x 4028049
= 1 x 3 x 2 x 4 x 3 x 5 x .....x 2006 x 2008 / 2x2 x 3 x3 x 4 x 4 x .....x 2007 x 2007
= ( 1 x 2 x 3 x .....x 2006) x ( 3 x 4 x 5 x .....x 2008) / ( 2 x 3 x 4 x ....x 2007) x ( 2 x 3 x 4 x ....x 2007)
= 2008 / 2007 x 2
= 1004 / 2007
Đúng 0
Bình luận (0)
Cho phương trình: x2 – (2m+1)x + m2 + m -2 0 (1) (m là tham số). Tìm m để phương trình (1) có 2 nghiệm phân biệt x1, x2 thoả mãn: x1(x1 -2x2) + x2(x2 -3x1) 9
Đọc tiếp
Cho phương trình: x2 – (2m+1)x + m2 + m -2 = 0 (1) (m là tham số). Tìm m để phương trình (1) có 2 nghiệm phân biệt x1, x2 thoả mãn:
x1(x1 -2x2) + x2(x2 -3x1) = 9
\(\Delta=\left(2m+1\right)^2-4\left(m^2+m-2\right)=9>0;\forall m\)
Phương trình luôn có 2 nghiệm pb với mọi m
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2m+1\\x_1x_2=m^2+m-2\end{matrix}\right.\)
\(x_1\left(x_1-2x_2\right)+x_2\left(x_2-2x_1\right)=9\)
\(\Leftrightarrow x_1^2+x_2^2-4x_1x_2=9\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-6x_1x_2=9\)
\(\Leftrightarrow\left(2m+1\right)^2-6\left(m^2+m-4\right)=9\)
\(\Leftrightarrow2m^2+2m-4=0\)
\(\Rightarrow\left[{}\begin{matrix}m=1\\m=-2\end{matrix}\right.\)
Đúng 1
Bình luận (0)