1) \(A=36x^2+12x+1=\left(6x+1\right)^2\ge0\)

\(minA=0\Leftrightarrow x=-\dfrac{1}{6}\)

2) \(B=9x^2+6x+1=\left(3x+1\right)^2\ge0\)

\(minB=0\Leftrightarrow x=-\dfrac{1}{3}\)

4) \(D=x^2-4x+y^2-8y+6=\left(x-2\right)^2+\left(y-4\right)^2-14\ge-14\) 

\(minD=-14\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=4\end{matrix}\right.\)

3) \(C=\left(x+1\right)\left(x-2\right)\left(x-3\right)\left(x-6\right)=\left(x^2-5x-6\right)\left(x^2-5x+6\right)=\left(x^2-5x\right)^2-36\ge-36\)

\(minC\Leftrightarrow\left[{}\begin{matrix}x=0\\x=5\end{matrix}\right.\)

5) \(E=\left(x-8\right)^2+\left(x+7\right)^2=2x^2-2x+113=2\left(x-\dfrac{1}{2}\right)^2+\dfrac{225}{2}\ge\dfrac{225}{2}\)

\(minE=\dfrac{225}{2}\Leftrightarrow x=\dfrac{1}{2}\)

e: Ta có: \(E=\left(x-8\right)^2+\left(x+7\right)^2\)

\(=x^2-16x+64+x^2+14x+49\)

\(=2x^2-2x+113\)

\(=2\left(x^2-x+\dfrac{113}{2}\right)\)

\(=2\left(x^2-2\cdot x\cdot\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{225}{4}\right)\)

\(=2\left(x-\dfrac{1}{2}\right)^2+\dfrac{225}{2}\ge\dfrac{225}{2}\forall x\)

Dấu '=' xảy ra khi \(x=\dfrac{1}{2}\)

Mình nghĩ ra câu C rồi bạn nào giúp mình nghĩ nốt câu A,B hộ mình nhé mình cảm ơn!

a:6x-5-9x^2

=-(9x^2-6x+5)

=-(9x^2-6x+1+4)

=-(3x-1)^2-4<=-4

=>A>=2/-4=-1/2

Dấu = xảy ra khi x=1/3

b: \(B=\dfrac{4x^2-6x+4-1}{2x^2-3x+2}=2-\dfrac{1}{2x^2-3x+2}\)

2x^2-3x+2=2(x^2-3/2x+1)

=2(x^2-2*x*3/4+9/16+7/16)

=2(x-3/4)^2+7/8>=7/8

=>-1/2x^2-3x+2<=-1:7/8=-8/7

=>B<=-8/7+2=6/7

Dâu = xảy ra khi x=3/4

a) \(\begin{cases}\left(x+2\right)^2\ge0\\\left(y-\frac{1}{5}\right)^2\ge0\end{cases}\Rightarrow\left(x+2\right)^2+\left(y-\frac{1}{5}\right)^2\ge0\)

\(\Leftrightarrow\left(x+2\right)^2+\left(y-\frac{1}{5}\right)^2-10\ge0-10=-10\)hay \(C\ge-10\)

Dấu "=" xảy ra khi:

\(\hept{\begin{cases}\left(x+2\right)^2=0\\\left(y-\frac{1}{5}\right)^2=0\end{cases}\Leftrightarrow\hept{\begin{cases}x+2=0\\y-\frac{1}{5}=0\end{cases}\Leftrightarrow}\hept{\begin{cases}x=-2\\y=\frac{1}{5}\end{cases}}}\)

Vậy GTNN C là -10 khi \(\hept{\begin{cases}x=-2\\y=\frac{1}{5}\end{cases}.}\)

b)\(\left(2x-3\right)^2\ge0\Rightarrow\left(2x-3\right)^2+5\ge0+5=5\)

\(\Rightarrow\frac{4}{\left(2x-3\right)^2-5}\le\frac{4}{5}\Leftrightarrow D\le\frac{4}{5}\)

Dấu "=" xảy ra khi:

\(\left(2x-3\right)^2=0\Rightarrow2x-3=0\Rightarrow2x=3\Rightarrow x=\frac{3}{2}\)

Vậy GTLN D là \(\frac{4}{5}\)khi \(x=\frac{3}{2}.\)

thank bạn nha

\(P=x^2-2x+5=x^2-2x+1+4=\left(x-1\right)^2+4\)

Vì \(\left(x-1\right)^2\ge0\Rightarrow\left(x-1\right)^2+4\ge4\)

=>P_min=(x-1)²+4=4

<=>(x-1)²=0

<=>x-1=0

<=>x=1

Vậy P_min=4 khi x=1

----------------------------------------------------------

\(Q=2x^2-6x=2\left(x^2-3x\right)=2\left[x^2-2.x.\frac{3}{2}+\left(\frac{3}{2}\right)^2\right]-\frac{9}{2}=2\left(x-\frac{3}{2}\right)^2-\frac{9}{2}\)

Vì \(\left(x-\frac{3}{2}\right)^2\ge0\Rightarrow2\left(x-\frac{3}{2}\right)^2\ge0\Rightarrow2\left(x-\frac{3}{2}\right)^2-\frac{9}{2}\ge-\frac{9}{2}\)

=>Q_min=\(2\left(x-\frac{3}{2}\right)^2-\frac{9}{2}=-\frac{9}{2}\)

<=>\(2\left(x-\frac{3}{2}\right)^2=0\)

<=>\(\left(x-\frac{3}{2}\right)^2=0\)

<=>\(x-\frac{3}{2}=0\)

<=>\(x=\frac{3}{2}\)

Vậy Q_min=\(-\frac{9}{2}\) khi \(x=\frac{3}{2}\)

Cảm ơn bạn nha

a)5a² +10ab+5b²

=5(a²+2ab+b²)

=5(a+b)²

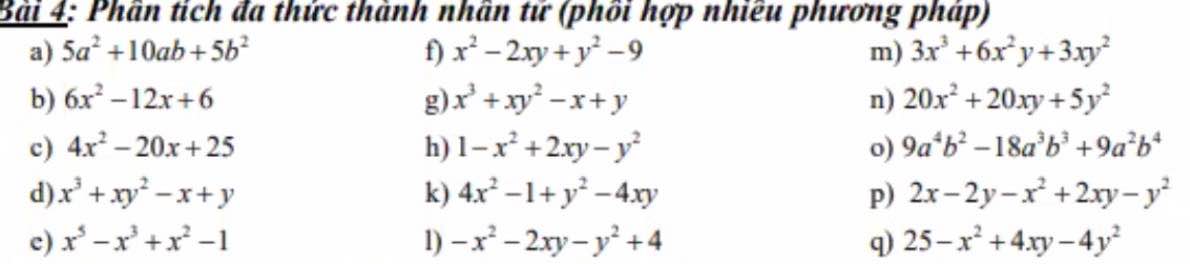
b.

\(6x^2-12x+6=6\left(x^2-2x+1\right)\)

\(=6\left(x-1\right)^2\)

c.

\(4x^2-20x+25\)

\(=\left(2x-5\right)^2\)

d. Câu này đề sai

e.

\(x^5-x^3+x^2-1\)

\(=x^3\left(x^2-1\right)+x^2-1\)

\(=\left(x^2-1\right)\left(x^3+1\right)\)

\(=\left(x-1\right)\left(x+1\right)\left(x+1\right)\left(x^2-x+1\right)\)

\(=\left(x-1\right)\left(x+1\right)^2\left(x^2-x+1\right)\)

f.

\(x^2-2xy+y^2-9\)

\(=\left(x-y\right)^2-9\)

\(=\left(x-y+3\right)\left(x-y-3\right)\)

g.

Câu này giống hệt câu d, và ko phân tích được

h.

\(1-x^2+2xy-y^2\)

\(=1-\left(x^2-2xy+y^2\right)\)

\(=1-\left(x-y\right)^2\)

\(=\left(1-x+y\right)\left(1+x-y\right)\)