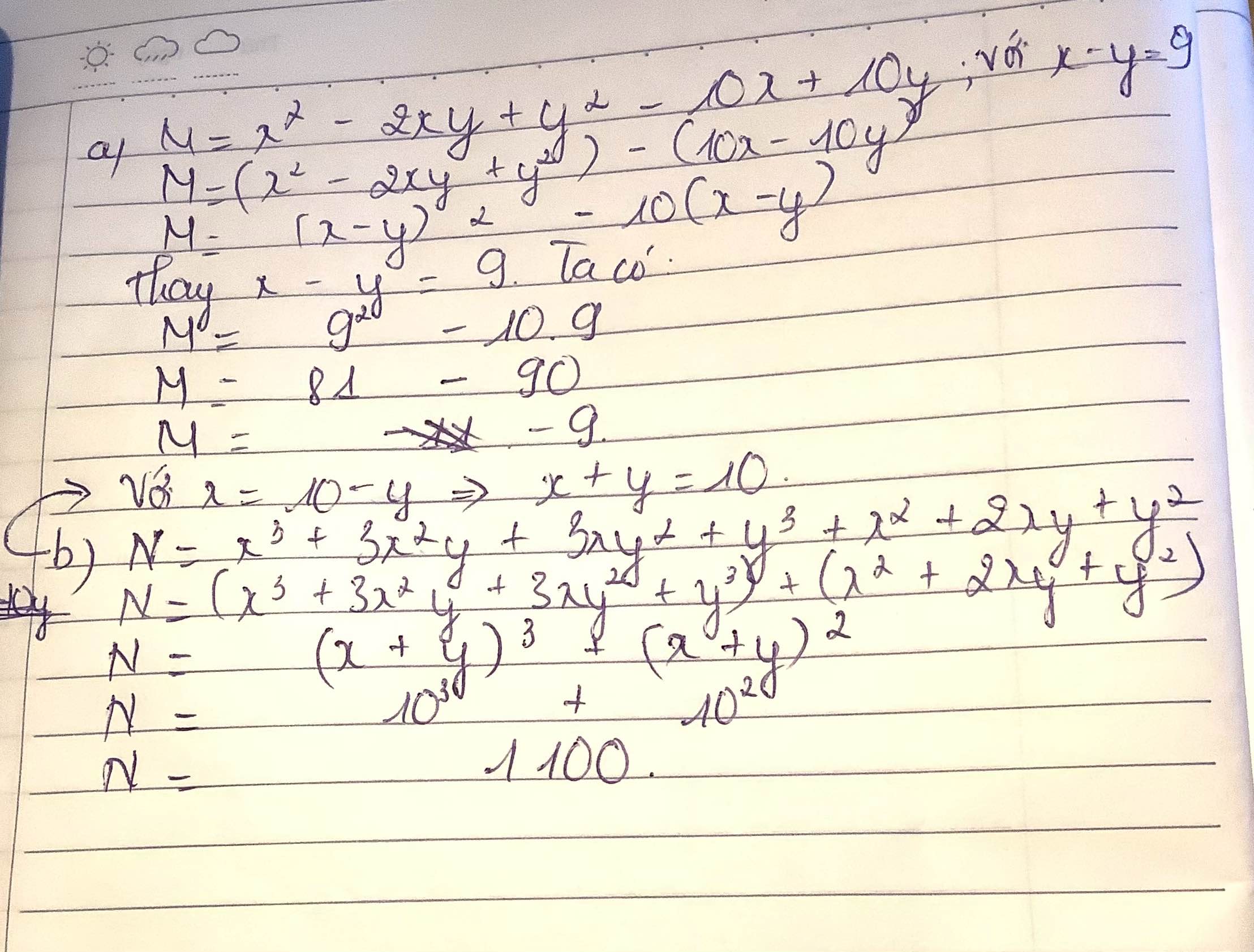b: \(B=x^3-8y^3-x^3+4x-4x+8y^3+2021=2021\)

Phân tích đa thức sau thành phân tử 

a, 4x³ - 10x² + 2x

b, x² - 3x + 2

Giúp mk vs m.n

Hình thang ABCD (AB//CD) có các tia phân giác của các góc A và D gặp nhau tại điểm E thuộc cạnh BC. Chứng minh rằng: 

a, AED = 90°

b, AD = AB + CD 

Giúp mình với mọi người :(((

\(A=x^2+4y^2-2xy+4x-10y+2020.\)

\(=\left(x^2-2xy+y^2\right)+\left(3y^2-6y+3\right)+\left(4x-4y\right)+2017\)

\(=\left(x-y\right)^2+3\left(y-1\right)^2+4\left(x-y\right)+2017\)

\(=\left[\left(x-y\right)^2+4\left(x-y\right)+4\right]+3\left(y-1\right)^2+2013\)

\(=\left(x-y+2\right)^2+3\left(y-1\right)^2+2013\)

\(A_{min}=2013\Leftrightarrow\hept{\begin{cases}\left(x-y+2\right)^2=0\\\left(y-1\right)^2=0\end{cases}}\)

\(\Leftrightarrow\hept{\begin{cases}x-y+2=0\\y=1\end{cases}\Rightarrow\hept{\begin{cases}x=-1\\y=1\end{cases}}}\)

\(B=8x^2+y^2-4xy-12x+2y+30\)

\(=\left(4x^2-4xy+y^2\right)+\left(4x^2-8x+4\right)-\left(4x-2y\right)+26\)

\(=\left(2x-y\right)^2+4\left(x-1\right)^2-2\left(2x-y\right)+26\)

\(=\left[\left(2x-y\right)^2-2\left(2x-y\right)+1\right]+4\left(x-1\right)^2+25\)

\(=\left(2x-y-1\right)^2+4\left(x-1\right)^2+25\)

\(\Rightarrow B_{min}=25\)\(\Leftrightarrow\hept{\begin{cases}\left(2x-y-1\right)^2=0\\\left(x-1\right)^2=0\end{cases}}\)

\(\Leftrightarrow\hept{\begin{cases}2x-y-1=0\\x=1\end{cases}}\)\(\Leftrightarrow x=y=1\)

Dồn biến thử xem sao :))

\(A=x^2+2.x.\left(2y-2\right)+\left(2y-2\right)^2-\left(2y-2\right)^2+10y^2-2y+20\)

\(=\left(x+2y-2\right)^2-4y^2+8y-4+10y^2-2y+20\)

\(=\left(x+2y-2\right)^2+6y^2+6y+16\)

.....

`A=x^2-4x+y^2-8y+6`

`A=x^2-4x+4+y^2-8y+16-14`

`A=(x-2)^2+(y-4)^2-14`

VÌ `(x-2)^2+(y-4)^2>=0`

`=>(x-2)^2+(y-4)^2-14>=-14`

`=>A>=-14`

Dấu "=" xảy ra khi `x-2=0,y-4=0<=>{(x=2),(y=4):}`

a)

\(A=4x-x^2+3=-\left(x^2-4x-3\right)=-\left(x^2-4x+4\right)+7=-\left(x-2\right)^2+7\le7\)

Daaus = xayr ra khi: x = 2

b) \(B=4x^2-12x+15=4\left(x^2-3x+9\right)-21=4\left(x-3\right)^2-21\ge-21\)

Dấu = xảy ra khi x = 3

c) \(C=4x^2+2y^2-4xy-4y+1=\left(4x^2-4xy+y^2\right)+\left(y^2-4y+4\right)-3=\left(2x-y\right)^2+\left(y-2\right)^2-3\ge-3\)

Dấu = xảy ra khi

2x = y và y = 2

=> x = 1 và y = 2

a) A = \(-x^2+4x+3=-\left(x-2\right)^2+7\le7\)

Dấu "=" <=> x = 2

b) \(4x^2-12x+15=\left(2x-3\right)^2+6\ge6\)

Dấu "=" xảy ra <=> \(x=\dfrac{3}{2}\)

c) \(4x^2+2y^2-4xy-4y+1\)

= \(\left(4x^2-4xy+y^2\right)+\left(y^2-4y+4\right)-3\)

= \(\left(2x-y\right)^2+\left(y-2\right)^2-3\ge-3\)

Dấu "=" <=> \(\left\{{}\begin{matrix}x=1\\y=2\end{matrix}\right.\)

Đây nè bạn.

a) Ta có: \(M=x^2-2xy+y^2-10x+10y\)

\(=\left(x-y\right)^2-10\left(x-y\right)\)

\(=9^2-10\cdot9=-9\)

a) \(C=4x^2+3y^2+4xy-4x-10y+7=\left[4x^2+4x\left(y-1\right)+\left(y-1\right)^2\right]+2\left(y^2-4y+4\right)-2=\left(2x+y-1\right)^2+2\left(y-2\right)^2-2\ge-2\)

\(minC=-2\Leftrightarrow\) \(\left\{{}\begin{matrix}x=-\dfrac{1}{2}\\y=2\end{matrix}\right.\)

d) \(D=x^2-2xy+6y^2-12x+2y+45=\left[x^2-2x\left(y+6\right)+\left(y+6\right)^2\right]+5\left(y^2-2y+1\right)+4=\left(x-y-6\right)^2+5\left(y-1\right)^2+4\ge4\)

\(minD=4\Leftrightarrow\) \(\left\{{}\begin{matrix}x=7\\y=1\end{matrix}\right.\)