Ta có :

21A=14B=6C=21A42=14B42=6C42=A2=B3=C7=A+B+C2+3+7=18012=1521A42=14B42=6C42=A2=B3=C7=A+B+C2+3+7=18012=15 

,mà A2=15=>A=15.2=30A2=15=>A=15.2=30

       B3=15=>B=15.3=45B3=15=>B=15.3=45

        C7=15=>C=15.7=105C7=15=>C=15.7=105

SUY RA GÓC A=30 ĐỘ ;GÓC B=45 ĐỘ; GÓC C=105 ĐỘ

k mik nha

TRỜI ! MỘT BÀI TOÁN BÙ ĐẦU BÙ ÓC

bài này lóp 7 hoc rù nhung quyen lop 7 nhình học giỏi lám đó

1.Cho tam giác ABC có số đo góc A,góc B,góc C tỉ lệ nghịch vs 3;4;6.Tính số đo các góc của tam giác ABC.

2.Cho tam giác ABC có số đo góc A,góc B,góc C tỉ lệ thuận vs 3;4;5.Tính số đo các góc của tam giác ABC.

không thấy câu hỏi nên không trả lời được nha

Theo bài ra ta có :

a + b = 24

b + c = 16

a + c = 14

=> b - a = 16 - 14 = 2

b = ( 24 + 2 ) : 2 = 13

a = 24 - 13 = 11

c = 14 - 11  = 3

Vậy a = 11 ; b = 13 ; c = 3

Ta có \(\begin{cases}\frac{\widehat{A}}{3}=\frac{\widehat{B}}{4}=\frac{\widehat{C}}{5}\\\widehat{A}+\widehat{B}+\widehat{C}=180^o\end{cases}\)

Áp dụng tính chất dãy tỉ số bằng nhau :

\(\frac{\widehat{A}}{3}=\frac{\widehat{B}}{4}=\frac{\widehat{C}}{5}=\frac{\widehat{A}+\widehat{B}+\widehat{C}}{3+4+5}=\frac{180^o}{12}=15\)

Suy ra \(\begin{cases}\widehat{A}=45^o\\\widehat{B}=60^o\\\widehat{C}=75^o\end{cases}\)

Xét tam giác ABC có : 

\(\widehat{A}+\widehat{B}+\widehat{C}=180^{\text{o}}\)

mà \(4.\widehat{A}=12.\widehat{B}=2.\widehat{C}\Rightarrow\hept{\begin{cases}4.\widehat{A}=12.\widehat{B}\\12.\widehat{B}=2.\widehat{C}\end{cases}\Rightarrow\hept{\begin{cases}\frac{\widehat{A}}{12}=\frac{\widehat{B}}{4}\\\widehat{\frac{B}{2}}=\frac{\widehat{C}}{12}\end{cases}}\Rightarrow\hept{\begin{cases}\frac{\widehat{A}}{12}=\frac{\widehat{B}}{4}\\\frac{\widehat{B}}{4}=\frac{\widehat{C}}{24}\end{cases}\Rightarrow}\frac{\widehat{A}}{12}=\frac{\widehat{B}}{4}=\frac{\widehat{C}}{24}}\)

Áp dụng tính chất của dãy tỉ số bằng nhau ta có : 

\(\frac{\widehat{A}}{12}=\frac{\widehat{B}}{4}=\frac{\widehat{C}}{24}=\frac{\widehat{A}+\widehat{B}+\widehat{C}}{12+4+24}=\frac{180^{\text{o}}}{40}=\frac{9^{\text{o}}}{2}\)

=> \(\hept{\begin{cases}\widehat{A}=54^{\text{o}}\\\widehat{B}=18^{\text{o}}\\\widehat{C}=108^{\text{o}}\end{cases}}\)

Chia cả ba đẳng thức ấy cho 12 bạn sẽ được

\(\frac{4\widehat{A}}{12}=\frac{12\widehat{B}}{12}=\frac{2\widehat{C}}{12}\)

Đơn giản thì bạn sẽ có

\(\frac{\widehat{A}}{3}=\frac{\widehat{B}}{1}=\frac{\widehat{C}}{6}\)

Theo đề ra có A+B+C=180 Vì  (độ) Tổng 3 góc của một tam giác (mình không để dấu mũ ở góc với ký hiệu độ nha bạn nhớ để vào)

Áp dụng tc dãy tỉ số bằng nhau

\(\frac{\widehat{A}}{3}=\frac{\widehat{B}}{1}=\frac{\widehat{C}}{6}=\frac{\widehat{A}+\widehat{B}+\widehat{C}}{3+1+6}=\frac{180}{10}=18\)

A=3x18=54

B=1x18=18

C=6x18=108

Vậy A=....

       B=.....

       C=.....

Nhớ để dấu mũ ở các góc và ký hiệu 

hoctot

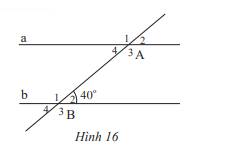
a) Góc ở vị trí so le trong với góc \(\widehat {{B_2}}\) là: \(\widehat {{A_4}}\)

Góc ở vị trí đồng vị với góc \(\widehat {{B_2}}\) là: \(\widehat {{A_2}}\)

b) Vì a // b nên:

+) \(\widehat {{A_4}} = \widehat {{B_2}}\)( 2 góc so le trong), mà \(\widehat {{B_2}} = 40^\circ \) nên \(\widehat {{A_4}} = 40^\circ \)

+) \(\widehat {{A_2}} = \widehat {{B_2}}\) ( 2 góc đồng vị), mà \(\widehat {{B_2}} = 40^\circ \) nên \(\widehat {{A_2}} = 40^\circ \)

Ta có: \(\widehat {{B_2}} + \widehat {{B_3}} = 180^\circ \) ( 2 góc kề bù) nên \(40^\circ  + \widehat {{B_3}} = 180^\circ  \Rightarrow \widehat {{B_3}} = 180^\circ  - 40^\circ  = 140^\circ \)

c) Ta có: \(\widehat {{B_2}} + \widehat {{B_1}} = 180^\circ \) ( 2 góc kề bù) nên \(40^\circ  + \widehat {{B_1}} = 180^\circ  \Rightarrow \widehat {{B_1}} = 180^\circ  - 40^\circ  = 140^\circ \)

Vì a // b nên \(\widehat {{A_1}} = \widehat {{B_1}}\) (2 góc đồng vị) nên \(\widehat {{A_1}} = 140^\circ \)