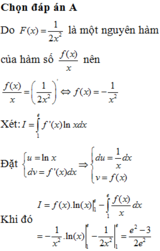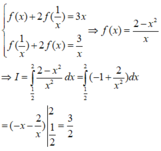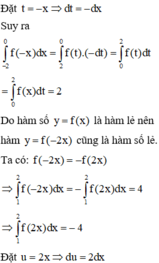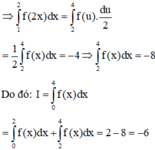Tính nguyên hàm của xdx/x^2+3x+2 .

Những câu hỏi liên quan
Mọi người giải giúp em câu này với ạ Tính nguyên hàm |xdx/x^2 +3 (đặt u=x^2 +3) Em cảm ơn ạ
Ta có: \(\int\dfrac{xdx}{x^2+3}\)
Đặt \(u=x^2+3\left(u>0\right)\)
Có \(du=2xdx\)
\(\Rightarrow\int\dfrac{xdx}{x^2+3}=\)\(\int\dfrac{du}{2u}=\dfrac{1}{2}ln\left(u\right)=\dfrac{1}{2}ln\left(x^2+3\right)\)
Đúng 4
Bình luận (1)
Tìm các nguyên hàm sau bằng phương pháp lấy nguyên hàm từng phần
a) \(I_1=\int x^22^xdx\)
b) \(I_2=\int x^2e^{3x}dx\)
c) \(I_3=\int e^{3x}\left(x^2-6x+2\right)dx\)
a) Đặt \(u=x^2\); \(dv=2^xdx\). Khi đó \(du=2xdx\) ; \(v=\int2^xdx=\frac{2^x}{\ln2}\) và \(I_1=x^2\frac{2^x}{\ln2}-\frac{2}{\ln2}\int x2^xdx\)
Lại áp dụng phép lấy nguyên hàm từng phần cho tích phân ở vế phải bằng cách đặt :
\(u=x\) ; \(dv=2^xdx\) và thu được \(du=dx\) ; \(v=\frac{2^x}{\ln2}\) Do đó
\(I_1=x^2\frac{2^x}{\ln_{ }2}-\frac{2}{\ln2}\left[x\frac{2^x}{\ln2}-\frac{1}{\ln2}\int2^xdx\right]\)
= \(x^2\frac{2^x}{\ln_{ }2}-\frac{2}{\ln2}\left[x\frac{2^x}{\ln2}-\frac{2^x}{\ln^22}\right]+C\) = \(\left(x^2-\frac{2}{\ln2}x+\frac{2}{\ln^22}\right)\frac{2^x}{\ln2}+C\)
Đúng 0
Bình luận (0)
b) Đặt \(u=x^2\); \(dv=e^{3x}dx\)
Khi đó \(du=2xdx\) ; \(v=\int e^{3x}dx=\frac{1}{3}\int e^{3x}d\left(3x\right)=\frac{1}{3}e^{ex}\)
Do đó:
\(I_2=\frac{x^2}{3}e^{3x}-\frac{1}{3}\int xe^{3x}dx\) (a)
Lại áp dụng phép lấy nguyên hàm từng phần cho nguyên hàm ở vế phải. Ta đặt \(u=x\) ; \(dv=e^{3x}dx\)
Khi đó \(du=dx\) ; \(v=\int e^{3x}dx=\frac{1}{3}e^{3x}\) và
\(\int xe^{ex}dx=\frac{x}{3}e^{3x}-\frac{1}{3}\int e^{3x}dx=\frac{x}{3}e^{3x}-\frac{1}{9}e^{3x}\)
Thế kết quả thu được vào (a) ta có :
\(I_2=\frac{x^2}{3}e^{3x}-\frac{2}{3}\left(\frac{x}{3}e^{3x}-\frac{1}{9}e^{3x}\right)+C=\frac{e^{3x}}{27}\left(9x^2-6x+2\right)+C\)
Đúng 0
Bình luận (0)
c) Đặt \(u=x^2-6x+2\); \(dv=e^{3x}dx\)
Khi đó \(du=\left(2x-6\right)dx\) ; \(v=\int e^{3x}dx=\frac{1}{3}e^{3x}\)
Do đó :
\(I_3=\frac{e^{3x}}{3}\left(x^2-6x+2\right)-\frac{2}{3}\int e^{3x}\left(x-3\right)dx\)
Đặt \(\int e^{3x}\left(x-3\right)dx=I'_3\)
Ta có \(\frac{e^{3x}}{3}\left(x^2-6x+2\right)-\frac{2}{3}I'_3\)(a)
Ta lại áp dụng phương pháp lấy nguyên hàm từng phần cho \(\int e^{3x}\left(x-3\right)dx\).
Đặt \(u=x-3\) ; \(dv=e^{3x}dx\)
Khi đó \(du=dx\); \(v=\int e^{3x}dx=\frac{e^{3x}}{3}\)
Vậy \(I'_3=\frac{e^{3x}}{3}\left(x-3\right)-\frac{1}{3}\int e^{3x}dx=\frac{e^{3x}}{3}\left(x-3\right)-\frac{1}{9}e^{3x}\)
Thế \(I'_3\) vào (a) ta thu được
\(I_3=e^{3x}\left(\frac{x^2}{3}-\frac{20}{9}x+\frac{38}{27}\right)+C\)
Đúng 0
Bình luận (0)
Nguyên hàm xdx/x^2+4x+8
\(\int\dfrac{xdx}{x^2+4x+8}=\dfrac{1}{2}\int\dfrac{2x+4}{x^2+4x+8}-2\int\dfrac{dx}{\left(x+2\right)^2+2^2}\)
\(=\dfrac{1}{2}ln\left(x^2+4x+8\right)-arctan\left(\dfrac{x+2}{2}\right)+C\)
Đúng 1
Bình luận (2)
Tính nguyên hàm
∫
ln
(
ln
x
)
x
d
x
Đọc tiếp
Tính nguyên hàm ∫ ln ( ln x ) x d x
![]()
![]()
![]()
![]()
Cho
F
x
1
2
x
2
là một nguyên hàm của hàm số
f
x
x
. Tính
∫
1
e
f
x
ln
x
d
x
bằng: A.
I...
Đọc tiếp
Cho F x = 1 2 x 2 là một nguyên hàm của hàm số f x x . Tính ∫ 1 e f ' x ln x d x bằng:
A. I = e 2 - 3 2 e 2
B. I = 2 - e 2 e 2
C. I = e 2 - 2 e 2
D. I = 3 - e 2 2 e 2
Cho hàm số f(x) liên tục trên R và
f
(
x
)
+
2
f
1
x
3
x
Tính tích phân
I
∫
1
2
1
f
(
x
)
x...
Đọc tiếp
Cho hàm số f(x) liên tục trên R và f ( x ) + 2 f 1 x = 3 x Tính tích phân I = ∫ 1 2 1 f ( x ) x d x
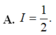
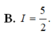
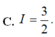
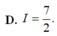
Sử dụng phương pháp tính nguyên hàm từng phần, hãy tính: ∫ x . ln 1 + x d x
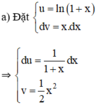
Theo công thức nguyên hàm từng phần ta có:
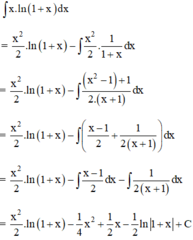
Đúng 0
Bình luận (0)
Áp dụng phương pháp tính nguyên hàm từng phần, hãy tính: ∫ x e - x d x
Cho hàm số y f(x) là hàm lẻ, liên tục trên [-4;4] biết
∫
-
2
0
f
-
x
d
x
2
và
∫
1
2
f
-
2
x
d
x
4
. Tính
∫
0...
Đọc tiếp
Cho hàm số y = f(x) là hàm lẻ, liên tục trên [-4;4] biết ∫ - 2 0 f - x d x = 2 và ∫ 1 2 f - 2 x d x = 4 . Tính ∫ 0 4 f x d x
A. I = -10
B. I = -6
C. I = 6
D. I = 10
Tìm họ nguyên hàm của hàm số sau
∫
x
2
+
1
.
x
d
x
A.
1
3
(
x
2
+
1
)
3
B. ...
Đọc tiếp
Tìm họ nguyên hàm của hàm số sau ∫ x 2 + 1 . x d x
A. 1 3 ( x 2 + 1 ) 3
B. 1 2 ( x 2 + 1 ) 3 + C
C. 1 3 ( x 2 + 1 ) 3 + C
D. 1 3 ( - x 2 + 1 ) 3 + C
Chọn C
Đặt u = x 2 + 1 ⇒ d u = 2 x d x ⇒ x d x = 1 2 d u
⇒ ∫ x 2 + 1 . x d x = ∫ u 1 2 . 1 2 d u = 1 2 ∫ u 1 2 d u = 1 2 u 3 2 . 2 3 = u 3 2 3 + C = 1 3 x 2 + 1 3 + C
Đúng 0
Bình luận (0)