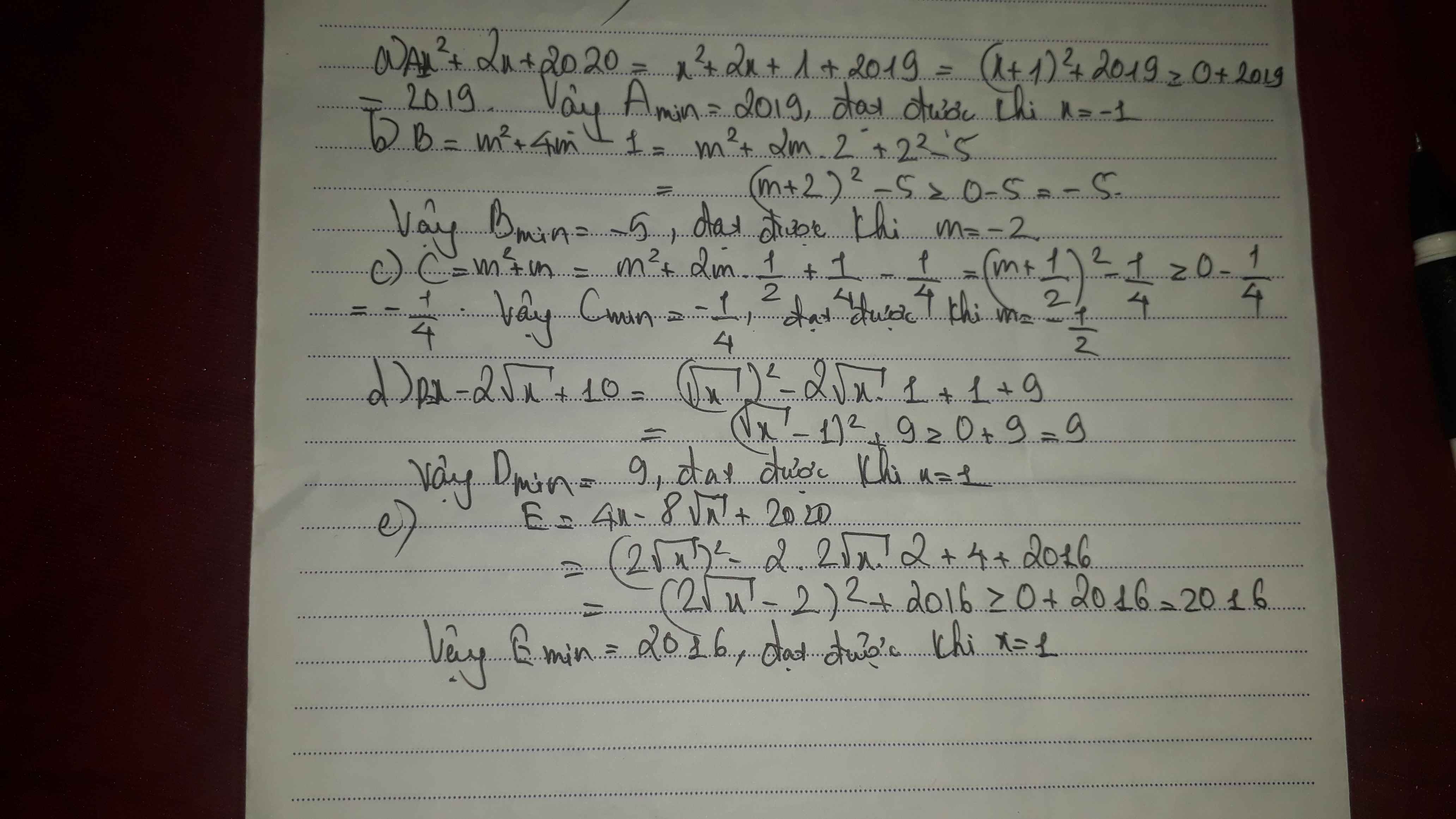\(a,=x^2+2x+1+2019=\left(x+1\right)^2+2019\ge2019\) dấu"=" xảy ra<=>x=-1

b,\(=m^2+2.2m+4-5=\left(m+2\right)^2-5\ge-5\) dấu"=" xảy ra<=>m=-2

c, \(=x-2\sqrt{x}+10=x-2\sqrt{x}+1+9=\left(\sqrt{x}-1\right)^2+9\ge9\)

dấu"=" xảy ra<=>x=1

b, \(4x-8\sqrt{x}+2020=4x-2.2.2\sqrt{x}+4+2016=\left(2\sqrt{x}-2\right)^2+2016\ge2016\)

dấu"=" xảy ra<=>x=1

a) Ta có: \(x^2+2x+2020\)

\(=x^2+2x+1+2019\)

\(=\left(x+1\right)^2+2019\ge2019\forall x\)

Dấu '=' xảy ra khi x=-1

b) Ta có: \(m^2+4m-1\)

\(=m^2+4m+4-5\)

\(=\left(m+2\right)^2-5\ge-5\forall m\)

Dấu '=' xảy ra khi m=-2

c) Ta có: \(m^2+m\)

\(=m^2+2\cdot m\cdot\dfrac{1}{2}+\dfrac{1}{4}-\dfrac{1}{4}\)

\(=\left(m+\dfrac{1}{2}\right)^2-\dfrac{1}{4}\ge-\dfrac{1}{4}\forall m\)

Dấu '=' xảy ra khi \(m=-\dfrac{1}{2}\)

:< rồi để căn nó mệt người mik đặt hem:P

Ta có: \(\hept{\begin{cases}\sqrt{a}=a\\\sqrt{b}=b\end{cases}}\)

\(P=a^2-2ab+3b^2-2a+1\)

\(\Leftrightarrow3P=3a^2-6ab+9b^2-6a+3\)

\(\Leftrightarrow3P=\left(x-3b\right)^2+2\left(a-\frac{3}{2}\right)^2-\frac{3}{2}\ge-\frac{3}{2}\)

\(\Rightarrow P\ge\frac{1}{2}\)

Dấu "=" xảy ra khi \(\hept{\begin{cases}a=\frac{3}{2}\\b=\frac{1}{2}\end{cases}}\) hay \(\hept{\begin{cases}a=\frac{9}{4}\\b=\frac{1}{4}\end{cases}}\)

Đặt \(\sqrt{a}=u;\sqrt{b}=v\left(u,v\ge0\right)\)

Lúc đó \(P=u^2-2uv+3v^2-2u+1\)

\(\Rightarrow3P=3u^2-6uv+9v^2-6u+3\)

\(=\left(u^2-6uv+9v^2\right)+2\left(u^2-6u+\frac{9}{4}\right)-\frac{3}{2}\)

\(=\left(u-3v\right)^2+2\left(u-\frac{3}{2}\right)^2-\frac{3}{2}\ge-\frac{3}{2}\)

\(\Rightarrow P\ge\frac{-1}{2}\)

(Dấu "=" khi \(\hept{\begin{cases}u=\frac{3}{2}\\v=\frac{1}{2}\end{cases}}\)\(\Rightarrow\hept{\begin{cases}\sqrt{a}=\frac{3}{2}\\\sqrt{b}=\frac{1}{2}\end{cases}}\Leftrightarrow\hept{\begin{cases}a=\frac{9}{4}\\b=\frac{1}{4}\end{cases}}\))

Phạm Mai Oanh

bạn sai vài chỗ cơ bản

+) Đặt ẩn phụ sai

+) GTNN của p là -1/2 chứ ko pk 1/2

binh phuong 2 ve giai ra

a.

\(A=\dfrac{2013}{x^2}-\dfrac{2}{x}+1=2013\left(\dfrac{1}{x}-\dfrac{1}{2013}\right)^2+\dfrac{2012}{2013}\ge\dfrac{2012}{2013}\)

Dấu "=" xảy ra khi \(x=2013\)

b.

\(B=\dfrac{4x^2+2-4x^2+4x-1}{4x^2+2}=1-\dfrac{\left(2x-1\right)^2}{4x^2+2}\le1\)

\(B_{max}=1\) khi \(x=\dfrac{1}{2}\)

\(B=\dfrac{-2x^2-1+2x^2+4x+2}{4x^2+2}=-\dfrac{1}{2}+\dfrac{\left(x+1\right)^2}{2x^2+1}\ge-\dfrac{1}{2}\)

\(B_{max}=-\dfrac{1}{2}\) khi \(x=-1\)

1) ta có

\(\sqrt{x-2}\ge0\)với mọi x 

=>A=1+\(\sqrt{x-2}\ge1\)

dấu "=" xảy ra khi:

x-2=0

<=>x=2

Vậy GTNN của A  là 1 tại x=2

2)

ta có :

\(-\sqrt{2x-1}\le0\)

=>B=5-\(\sqrt{2x-1}\le5\)

Dấu "=" xảy ra khi:

2x-1=0

<=>2x=1

<=>x=1/2

Vậy GTLN của B là 5 tại x=1/2