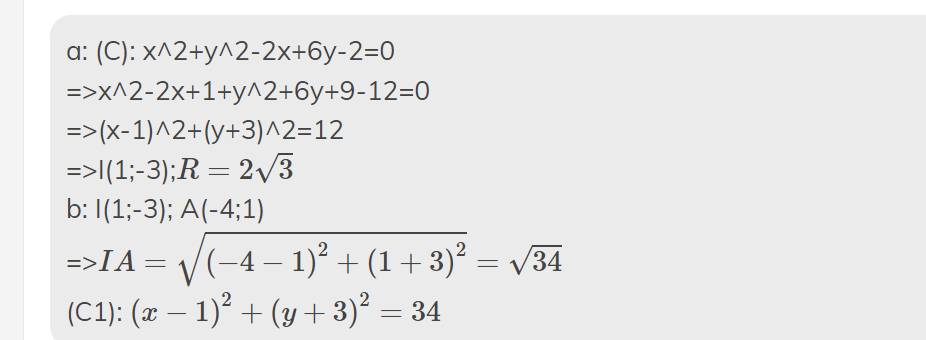Trong mặt phẳnng tọa độ Oxy cho đường tròn (C) có phương trình \(x^2+y^2-2x+4y+1=0\) và điểm A(1;-3). Tìm toạ độ điểm M thuộc đường tròn (C) sao cho độ dài đoạn MA lớn nhất

Những câu hỏi liên quan
Câu 20: Trong mặt phăng tọa độ Oxy, cho điểm I(4;3), đường thăng d:3x+4y-4=0 và đường tròn (C):x²+y²-2x+6y-2=0.
a) Tìm tọa độ tâm và bán kính R của đường tròn (C).
b) Viết phương trình đường tròn có tâm I và đi qua A(-4;1)
c) Viết phương trình đườNg tròn (C') có tâm là I và cắt d tại hai điếm M, N sao cho MN =6
a) Để tìm tọa độ tâm và bán kính của đường tròn ©, ta cần viết lại phương trình của nó dưới dạng chuẩn:
\begin{align*}
x^2 + y^2 - 2x + 6y - 2 &= 0 \
\Leftrightarrow (x-1)^2 + (y+3)^2 &= 14
\end{align*}
Vậy, tọa độ tâm của đường tròn © là $(1,-3)$ và bán kính của đường tròn © là $\sqrt{14}$.
b) Đường tròn có tâm $I(4,3)$ và đi qua $A(-4,1)$ có phương trình là:
$$(x-4)^2 + (y-3)^2 = (-4-4)^2 + (1-3)^2 = 20$$
c) Để tìm phương trình đường tròn (C') có tâm là $I(4,3)$ và cắt đường thẳng $d: 3x+4y-4=0$ tại hai điểm $M$ và $N$ sao cho $MN=6$, ta có thể làm như sau:
Tìm giao điểm $H$ của đường thẳng $d$ và đường vuông góc với $d$ đi qua $I$.Tìm hai điểm $M$ và $N$ trên đường thẳng $d$ sao cho $HM=HN=3$.Xây dựng đường tròn (C') có tâm là $I$ và bán kính bằng $IN=IM=\sqrt{3^2+4^2}=5$.
Để tìm giao điểm $H$, ta cần tìm phương trình của đường thẳng vuông góc với $d$ đi qua $I$. Đường thẳng đó có phương trình là:
$$4x - 3y - 7 = 0$$
Giao điểm $H$ của đường thẳng này và $d$ có tọa độ là $(\frac{52}{25}, \frac{9}{25})$.
Để tìm hai điểm $M$ và $N$, ta có thể sử dụng công thức khoảng cách giữa điểm và đường thẳng. Khoảng cách từ điểm $H$ đến đường thẳng $d$ là:
$$d(H,d) = \frac{|3\cdot \frac{52}{25} + 4\cdot \frac{9}{25} - 4|}{\sqrt{3^2+4^2}} = \frac{1}{5}$$
Vậy, hai điểm $M$ và $N$ cách $H$ một khoảng bằng $\frac{3}{5}$ và $\frac{4}{5}$ đơn vị theo hướng vuông góc với $d$. Ta có thể tính được tọa độ của $M$ và $N$ như sau:
$$M = \left(\frac{52}{25} - \frac{4}{5}\cdot 4, \frac{9}{25} + \frac{3}{5}\cdot 3\right) = \left(\frac{12}{25}, \frac{54}{25}\right)$$
và
$$N = \left(\frac{52}{25} + \frac{4}{5}\cdot 4, \frac{9}{25} + \frac{4}{5}\cdot 3\right) = \left(\frac{92}{25}, \frac{27}{5}\right)$$
Cuối cùng, phương trình đường tròn (C') có tâm là $I(4,3)$ và cắt đường thẳng $d$ tại hai điểm $M$ và $N$ sao cho $MN=6$ là:
$$(x-4)^2 + (y-3)^2 = 5^2$$
Đúng 0
Bình luận (0)
Câu 20: Trong mặt phăng tọa độ Oxy, cho điểm I(4;3), đường thăng d:3x+4y-4=0 và đường tròn (C):x²+y²-2x+6y-2=0.
a) Tìm tọa độ tâm và bán kính R của đường tròn (C).
b) Viết phương trình đường tròn có tâm I và đi qua A(-4;1)
c) Viết phương trình đườNg tròn (C') có tâm là I và cắt d tại hai điếm M, N sao cho MN =6
Giải thích cụ thể câu c cho mình.
a: (C): x^2+y^2-2x+6y-2=0
=>x^2-2x+1+y^2+6y+9-12=0
=>(x-1)^2+(y+3)^2=12
=>I(1;-3);\(R=2\sqrt{3}\)
b: I(1;-3); A(-4;1)
=>\(IA=\sqrt{\left(-4-1\right)^2+\left(1+3\right)^2}=\sqrt{34}\)
(C1): \(\left(x-1\right)^2+\left(y+3\right)^2=34\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Câu 20: Trong mặt phăng tọa độ Oxy, cho điểm I(4;3), đường thăng d:3x+4y-4=0 và đường tròn (C):x²+y²-2x+6y-2=0.
a) Tìm tọa độ tâm và bán kính R của đường tròn (C).
b) Viết phương trình đường tròn có tâm I và đi qua A(-4;1)
c) Viết phương trình đườNg tròn (C') có tâm là I và cắt d tại hai điếm M, N sao cho MN =6
Giải thích cụ thể câu c cho mình.
Trong mặt phẳng tọa độ Oxy cho điểm A(4; – 1), đường thẳng (d) : 3x – 2y + 1 = 0 và đường tròn (C) :
x^2 + y^2 - 2x + 4y -4 = 0
a. Tìm tọa độ A’ và phương trình (d’) lần lượt là ảnh của A và (d) qua phép tịnh tiến theo vectơ v = (– 2; 3)
b. Tìm phương trình đường tròn (C’) là ảnh của đường tròn (C) qua phép đối xứng trục là đường thẳng (D) : x – y = 0
1. Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có cạnh AC đi qua điểm M (0;-1). Biết AB 2AM, phương trình đường phân giác trong AD : x-y 0, phương trìn đường cao CH: 2x+y+3 0. Tìm tọa độ các đỉnh A,B,C.2. Trong mặt phẳng tọa độ Oxy, cho hình vuông ABCD tâm I (-1;1). Gọi M nằm trên cạnh CD sao cho MC 2 MD. Tìm tọa độ điểm C biết đường thẳng AM có phương trình 2x-y0,điểm A có hoành độ dương
Đọc tiếp
1. Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có cạnh AC đi qua điểm M (0;-1). Biết AB =2AM, phương trình đường phân giác trong AD : x-y =0, phương trìn đường cao CH: 2x+y+3 =0. Tìm tọa độ các đỉnh A,B,C.
2. Trong mặt phẳng tọa độ Oxy, cho hình vuông ABCD tâm I (-1;1). Gọi M nằm trên cạnh CD sao cho MC =2 MD. Tìm tọa độ điểm C biết đường thẳng AM có phương trình 2x-y=0,điểm A có hoành độ dương
Trong mặt phẳng tọa độ Oxy, cho đường tròn C có phương trình : x^2 + y^2 - 12x - 4y + 36 = 0. Viết phương trình đường tròn C1 tiếp xúc với hai trục tọa độ Ox, Oy đồng thời tiếp xúc với C.
Trong mặt phẳng tọa độ Oxy, cho đường tròn (C):
x
2
+
y
2
+
2
x
-
4
y
+
1
0
. Ảnh của đường tròn (C) qua phép vị tự tâm O tỷ số k-2 có phương trình là A.
x
2
+
y
2
+
4
x
-
8...
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho đường tròn (C): x 2 + y 2 + 2 x - 4 y + 1 = 0 . Ảnh của đường tròn (C) qua phép vị tự tâm O tỷ số k=-2 có phương trình là
A. x 2 + y 2 + 4 x - 8 y + 4 = 0
B. x 2 + y 2 - 4 x + 8 y + 4 = 0
C. x 2 + y 2 + 4 x - 8 y + 4 = 0
D. x 2 + y 2 + 4 x - 8 y + 2 = 0
Trong mặt phẳng tọa độ Oxy, cho đường tròn
C
:
x
2
+
y
2
+
2
x
-
4
y
+
1
0
. Ảnh của đường tròn (C) qua phép vị tự tâm O tỷ sốk 2 có phương trình là A.
x
2
+
y
2
+
4
x
-
8
y...
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho đường tròn C : x 2 + y 2 + 2 x - 4 y + 1 = 0 . Ảnh của đường tròn (C) qua phép vị tự tâm O tỷ số
k = 2 có phương trình là
A. x 2 + y 2 + 4 x - 8 y + 4 = 0
B. x 2 + y 2 - 4 x + 8 y + 4 = 0
C. x 2 + y 2 + 4 x - 8 y - 4 = 0
D. x 2 + y 2 + 4 x - 8 y + 2 = 0
Trong mặt phẳng tọa độ Oxy, cho điểm M(3; -5), đường thẳng d có phương trình \(3x+2y-6=0\) và đường tròn (C) có phương trình \(x^2+y^2-2x+4y-4=0\). Tìm ảnh của M, d và (C) qua phép đối xứng qua trục Ox ?