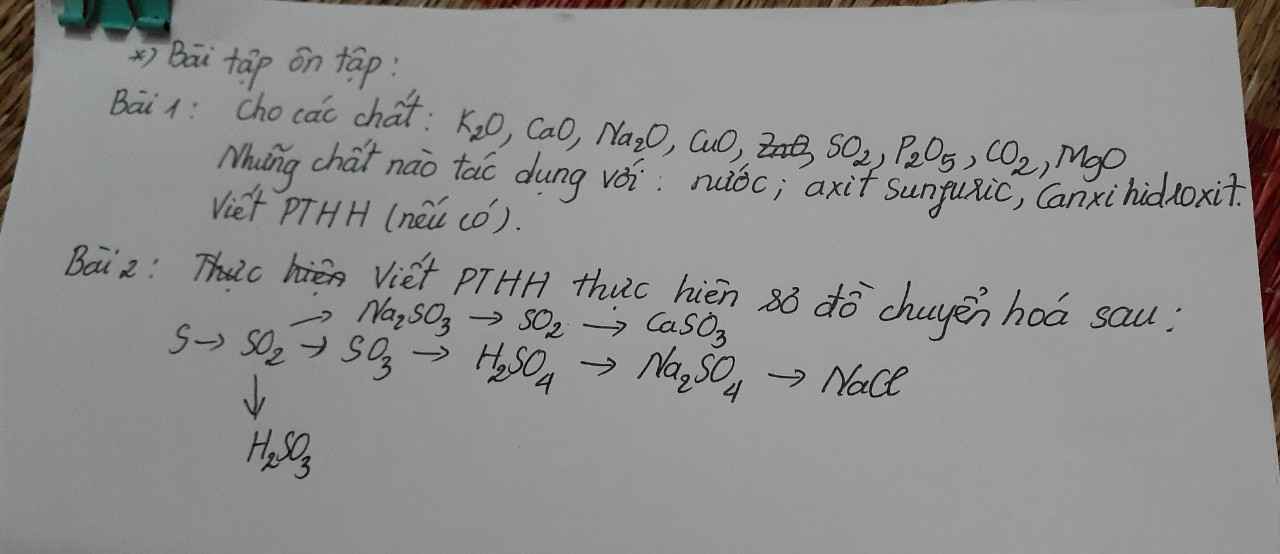
giải hộ mình bài 1 với ạ
giải hộ mình bài 1 với ạ
Có hai bài toán công nghệ, 1 bài về động cơ 2 kỳ, 1 bài về động cơ 4 kỳ, mọi người giải hộ mình với ạ ( không cần giải cụ thể, mình chỉ cần giúp hướng dẫn giải thôi ạ)

Giải hộ mình câu c bài này với ạ, mình cảm ơn nhiều nhiều ^^
Mình đag cần gấp, làm nhanh hộ mình với ạ <3

Giải hộ mình bài bày với ạ, mình cảm ơn nhiều ạ ^^ <3 
a) Phương trình hoành độ giao điểm là:
\(x^2=\left(m+2\right)x-2m\)
\(\Leftrightarrow x^2-\left(m+2\right)x+2m=0\)
\(\Delta=\left(m+2\right)^2-8m=m^2+4m+4-8m=m^2-4m+4=\left(m-2\right)^2\)
Để (d) và (P) cắt nhau tại hai điểm phân biệt thì \(\Delta>0\)
\(\Leftrightarrow\left(m-2\right)^2>0\)
mà \(\left(m-2\right)^2\ge0\)
nên \(m-2\ne0\)
hay \(m\ne2\)
Vậy: Để (d) và (P) cắt nhau tại hai điểm phân biệt thì \(m\ne2\)
Giải hộ mình câu c bài này với ạ, mình cảm ơn nhiều nhiều ^^
Mình đag cần gấp lắm ạ, làm nhanh hộ mình với <3
Cảm ơn lần nữa

1) Vì x=25 thỏa mãn ĐKXĐ nên Thay x=25 vào biểu thức \(A=\dfrac{\sqrt{x}-2}{x+1}\), ta được:
\(A=\dfrac{\sqrt{25}-2}{25+1}=\dfrac{5-2}{25+1}=\dfrac{3}{26}\)
Vậy: Khi x=25 thì \(A=\dfrac{3}{26}\)
2) Ta có: \(B=\dfrac{\sqrt{x}-3}{\sqrt{x}+1}+\dfrac{2x+8\sqrt{x}-6}{x-\sqrt{x}-2}\)
\(=\dfrac{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}+\dfrac{2x+8\sqrt{x}-6}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{x-5\sqrt{x}+6+2x+8\sqrt{x}-6}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{3x+3\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{3\sqrt{x}\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{3\sqrt{x}}{\sqrt{x}-2}\)
 giải hộ mình mấy bài này vs ạ !
giải hộ mình mấy bài này vs ạ !
giải hộ mình mấy bài này vs ạ !
Bài 5 hình 1: (tự vẽ hình nhé bạn)
a) Xét ΔABD và ΔACB ta có:
\(\widehat{BAD}\)= \(\widehat{BAC}\) (góc chung)
\(\widehat{ABD}\)= \(\widehat{ACB}\) (gt)
=> ΔABD ~ ΔACB (g-g)
=> \(\dfrac{AB}{AC}\) = \(\dfrac{BD}{CB}\) = \(\dfrac{AD}{AB}\) (tsđd)
b) Ta có: \(\dfrac{AB}{AC}\) = \(\dfrac{AD}{AB}\) (cm a)
=> \(AB^2\) = AD.AC
=> \(2^2\) = AD.4
=> AD = 1 (cm)
Ta có: AC = AD + DC (D thuộc AC)
=> 4 = 1 + DC
=> DC = 3 (cm)
c) Xét ΔABH và ΔADE ta có:
\(\widehat{AHB}\) = \(\widehat{AED}\) (=\(90^0\))
\(\widehat{ADB}\) = \(\widehat{ABH}\) (ΔABD ~ ΔACB)
=> ΔABH ~ ΔADE
=> \(\dfrac{AB}{AD}\) = \(\dfrac{AH}{AE}\) = \(\dfrac{BH}{DE}\) (tsdd)
Ta có: \(\dfrac{S_{ABH}}{S_{ADE}}\) = \(\left(\dfrac{AB}{AD}\right)^2\)= \(\left(\dfrac{2}{1}\right)^2\)= 4
=> đpcm
Tiếp bài 5 hình 2 (tự vẽ hình)
a) Xét ΔABC vuông tại A ta có:
\(BC^2\) = \(AB^2\) + \(AC^2\)
\(BC^2\) = \(21^2\) + \(28^2\)
BC = 35 (cm)
b) Xét ΔABC và ΔHBA ta có:
\(\widehat{BAC}\) = \(\widehat{AHB}\) ( =\(90^0\))
\(\widehat{ABC}\) = \(\widehat{ABH}\) (góc chung)
=> ΔABC ~ ΔHBA (g-g)
=> \(\dfrac{AB}{BH}\) = \(\dfrac{BC}{AB}\) (tsdd)
=> \(AB^2\) = BH.BC
=> \(21^2\) = 35.BH
=> BH = 12,6 (cm)
c) Xét ΔABC ta có:
BD là đường p/g (gt)
=> \(\dfrac{AD}{DC}\) = \(\dfrac{AB}{BC}\) (t/c đường p/g)
Xét ΔABH ta có:
BE là đường p/g (gt)
=> \(\dfrac{HE}{AE}\) = \(\dfrac{BH}{AB}\) (t/c đường p/g)
Mà: \(\dfrac{AB}{BC}\) = \(\dfrac{BH}{AB}\) (cm b)
=> đpcm
d) Ta có: \(\left\{{}\begin{matrix}\widehat{HBE}+\widehat{BEH}=90^0\\\widehat{ABD}+\widehat{ADB=90^0}\\\widehat{HBE}=\widehat{ABD}\end{matrix}\right.\)
=> \(\widehat{BEH}=\widehat{ADB}\)
Mà \(\widehat{BEH}=\widehat{AED}\) (2 góc dd)
Nên \(\widehat{ADB}=\widehat{AED}\)
=> đpcm
Ai giúp mình bài này với ạ!!! Giải chi tiết hộ mình nhé! Mình cảm ơn ạ!!!
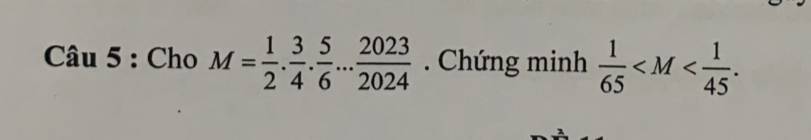
Giải hộ mình bài này với ạ mình cần gấp 
Sửa đề là : 4.6 (g)
\(n_{H_2}=\dfrac{2.24}{22.4}=0.1\left(mol\right)\)
\(A+H_2O\rightarrow AOH+\dfrac{1}{2}H_2\)
\(0.2...............................0.1\)
\(M_A=\dfrac{4.6}{0.2}=23\left(\dfrac{g}{mol}\right)\)
\(A:Na\)
Đề này C1 em sửa thành 4,6 gam kim loại như bạn dưới, C2 em sửa thành 22,4 lít H2
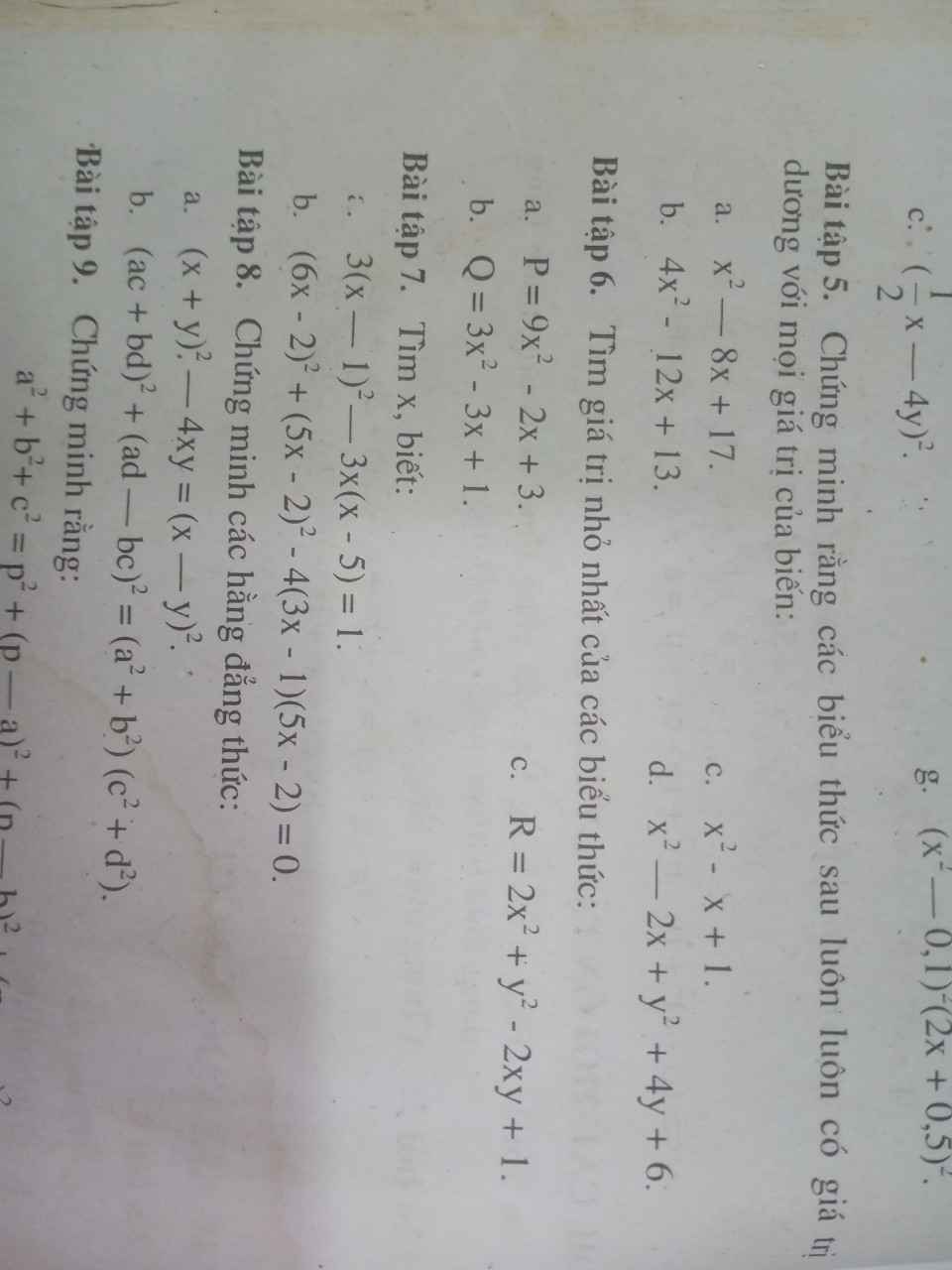
GIẢI HỘ MÌNH BÀI 5 VỚI 6 VỚI Ạ!
Bài 5:
a: Ta có: x2−8x+17x2−8x+17
=x2−8x+16+1=x2−8x+16+1
=(x−4)2+1>0∀x=(x−4)2+1>0∀x
b: Ta có: 4x2−12x+134x2−12x+13
=4x2−12x+9+4=4x2−12x+9+4
=(2x−3)2+4>0∀x=(2x−3)2+4>0∀x
c: Ta có: x2−x+1x2−x+1
=(x−12)2+34>0∀x
Bài 5:
a: Ta có: \(x^2-8x+17\)
\(=x^2-8x+16+1\)
\(=\left(x-4\right)^2+1>0\forall x\)
b: Ta có: \(4x^2-12x+13\)
\(=4x^2-12x+9+4\)
\(=\left(2x-3\right)^2+4>0\forall x\)
c: Ta có: \(x^2-x+1\)
\(=x^2-2\cdot x\cdot\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{3}{4}\)
\(=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}>0\forall x\)
Bài 5:
a. $x^2-8x+17=(x^2-8x+16)+1=(x-4)^2+1$
$\geq 0+1>0$ với mọi $x\in\mathbb{R}$ (đpcm)
b. $4x^2-12x+13=(4x^2-12x+9)+4$
$=(2x-3)^2+4\geq 0+4>0$ với mọi $x\in\mathbb{R}$ (đpcm)
c. $x^2-x+1=(x^2-x+\frac{1}{4})+\frac{3}{4}$
$=(x-\frac{1}{2})^2+\frac{3}{4}\geq \frac{3}{4}>0$ với mọi $x\in\mathbb{R}$ (đpcm)
d.
$x^2-2x+y^2+4y+6=(x^2-2x+1)+(y^2+4y+4)+1$
$\geq (x-1)^2+(y+2)^2+1$
$\geq 0+0+1>0$ với mọi $x,y\in\mathbb{R}$