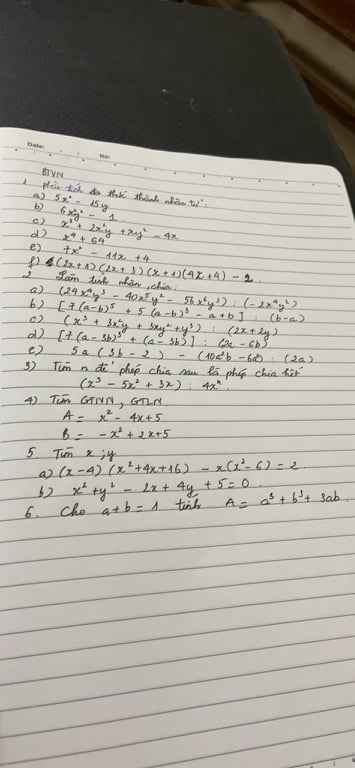Bài 5:
a: Ta có: x2−8x+17x2−8x+17
=x2−8x+16+1=x2−8x+16+1
=(x−4)2+1>0∀x=(x−4)2+1>0∀x
b: Ta có: 4x2−12x+134x2−12x+13
=4x2−12x+9+4=4x2−12x+9+4
=(2x−3)2+4>0∀x=(2x−3)2+4>0∀x
c: Ta có: x2−x+1x2−x+1
=(x−12)2+34>0∀x
Bài 5:
a: Ta có: \(x^2-8x+17\)
\(=x^2-8x+16+1\)
\(=\left(x-4\right)^2+1>0\forall x\)
b: Ta có: \(4x^2-12x+13\)
\(=4x^2-12x+9+4\)
\(=\left(2x-3\right)^2+4>0\forall x\)
c: Ta có: \(x^2-x+1\)
\(=x^2-2\cdot x\cdot\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{3}{4}\)
\(=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}>0\forall x\)
Bài 5:
a. $x^2-8x+17=(x^2-8x+16)+1=(x-4)^2+1$
$\geq 0+1>0$ với mọi $x\in\mathbb{R}$ (đpcm)
b. $4x^2-12x+13=(4x^2-12x+9)+4$
$=(2x-3)^2+4\geq 0+4>0$ với mọi $x\in\mathbb{R}$ (đpcm)
c. $x^2-x+1=(x^2-x+\frac{1}{4})+\frac{3}{4}$
$=(x-\frac{1}{2})^2+\frac{3}{4}\geq \frac{3}{4}>0$ với mọi $x\in\mathbb{R}$ (đpcm)
d.
$x^2-2x+y^2+4y+6=(x^2-2x+1)+(y^2+4y+4)+1$
$\geq (x-1)^2+(y+2)^2+1$
$\geq 0+0+1>0$ với mọi $x,y\in\mathbb{R}$
Bài 6:
a. $P=9x^2-2x+3=(3x)^2-2.3x.\frac{1}{3}+\frac{1}{3^2}+\frac{26}{9}$
$=(3x-\frac{1}{3})^2+\frac{26}{9}\geq 0+\frac{26}{9}=\frac{26}{9}$
Vậy $P_{\min}=\frac{26}{9}$ khi $3x-\frac{1}{3}=0$
$\Leftrightarrow x=\frac{1}{9}$
b.
$Q=3x^2-3x+1=3(x^2-x+\frac{1}{4})+\frac{1}{4}$
$=3(x-\frac{1}{2})^2+\frac{1}{4}\geq \frac{1}{4}$
Vậy $Q_{\min}=\frac{1}{4}$ khi $x-\frac{1}{2}=0\Leftrightarrow x=\frac{1}{2}$
c.
$R=2x^2+y^2-2xy+1=x^2+(x^2-2xy+y^2)+1$
$=x^2+(x-y)^2+1\geq 0+0+1=1$
Vậy $R_{\min}=1$ khi $x=x-y=0$
$\Leftrightarrow x=y=0$

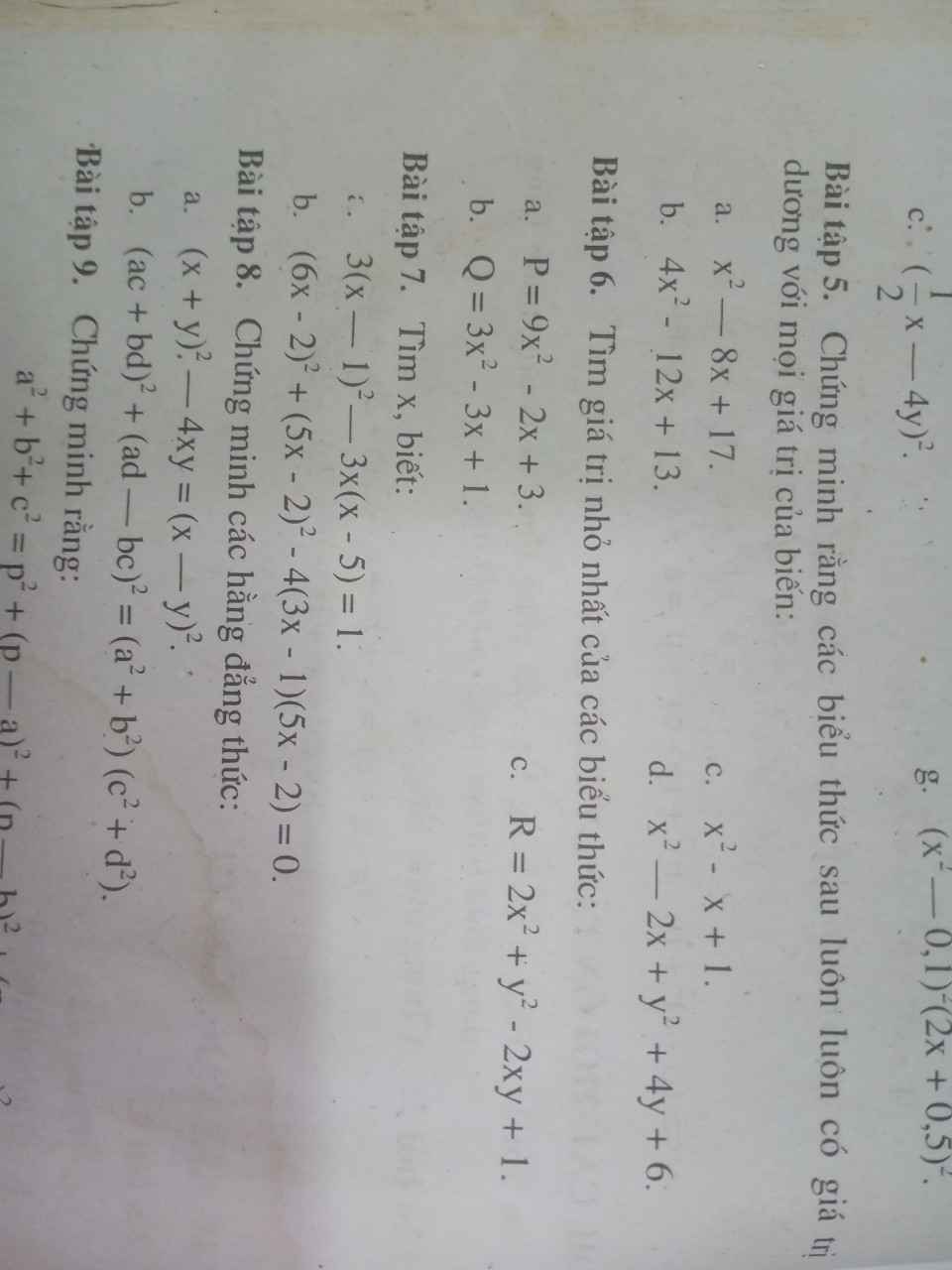





 \
\
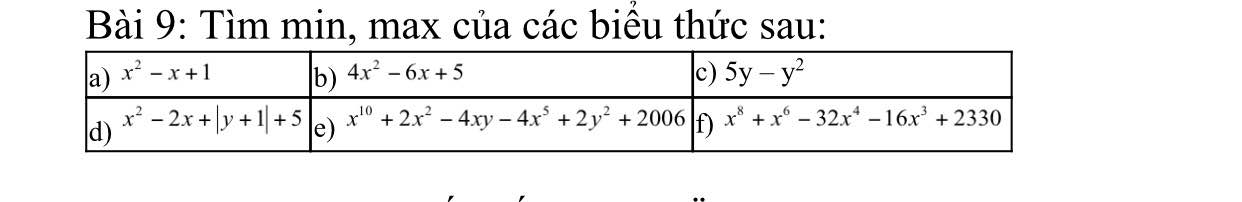

 giải hộ mình mấy bài này vs ạ !
giải hộ mình mấy bài này vs ạ !