cho tứ giác ABCD có E,F theo thứ tự là trọng điểm của AD,BC.Cm EF ≤ AB+DC/2
cho tứ giác ABCD có E,F theo thứ tự là trọng điểm của AD,BC.Cm EF ≤ AB+DC/2
cho hình thang ABCD có E,F theo thứ tự là trọng điểm của AD,BC.Cm EF ≤ \(AB+DC/2\)
Xét hình thang ABCD có:
AE = DE
BF = CF
=> EF là đường trung bình của hình thang ABCD
=> EF// AB và DC (1)
Mà : K ∈ EF (2)
Từ (1), (2) => EK // DC
Xét tam giác ADC có
AE = DE
EK// DC
=> AK = CK
Xét hình thang ABCD có
E là trung điểm của AD
F là trung điểm của BC
Do đó: EF là đường trung bình của hình thang ABCD
Suy ra: \(FE=\dfrac{AB+CD}{2}\)
cho hình thang ABCD có E,F theo thứ tự là trọng điểm của AD,BC.Cm EF ≤ AB+DC/2
E,F là trung điểm của AD và BC
=> EF là đường trung bình của hình thang ABCD
=> \(EF=\dfrac{AB+CD}{2}\)
cho hình thang ABCD có E,F theo thứ tự là trung điểm của AD,BC.Cm EF ≤ AB+DC/2
Tham khảo đây nha:
https://hoidap247.com/cau-hoi/1107494
Tứ giác ABCD có E,F theo thứ tự là trung điểm của AD,BC
a. Chứng minh rằng : EF< hoặc = AB+CD /2
b. Tứ giác ABCD có điều kiện gì thì EF=AB+CD/2
Cho tứ giác ABCD có AD=BC, gọi E và F theo thứ tự là trung điểm của AB, CD, O là giao điểm của AD và BC, H:G theo thứ tự là giao điểm của EF với OD,OC. Chứng minh OG=OH
Trên tia đối của ED lấy điểm K sao cho E là trung điểm của DK.
Xét \(\Delta\)DAE=\(\Delta\)KBE (c.g.c) => AD=BK (2 cạnh tương ứng)
Mà AD=BC => BK=BC => \(\Delta\)BKC cân tại B => ^BCK=(1800-^KBC)/2 (1)
Lại có: ^DAE=^KBE (2 góc tương ứng) => AD//BK (2 góc so le trg bằng nhau)
hay OH//BK => ^HOG=^KBC ( Đồng vị) (2)
E là trung điểm DK; F là trung điểm DC => EF là đường trung bình \(\Delta\)DKC
=> EF//KC hay HG//KC => ^OGH=^BCK (3)
Thay (2) và (3) vào (1); ta được: ^OGH=(1800-^HOG)/2 => \(\Delta\)HOG cân tại O
=> OG=OH (đpcm)
Cho tứ giác ABCD có M,N,E,F theo thứ tự là trung điểm của AB, BC, CD, AD. Chứng minh, MN // EF, MF// NE.
Ta có M,N là trung điểm của AB,BC
Suy ra : MN là đường trung bình của Tam giác ABC
Suy ra : MN = AC chia 2 và MN // EF
C/m tương tự : MF // NE
Cho tứ giác ABCD. Gọi E, F, I theo thứ tự là trung điểm của AD, BC, AC.
Chứng minh rằng:
a) EI//CD, IF//AB.
b)EF=<AB+CD/2
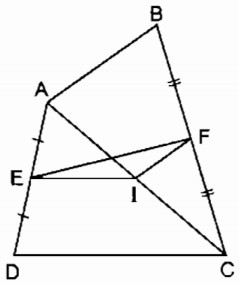
a) Trong tam giác ADC, ta có:
E là trung điểm của AD (gt)
I là trung điểm của AC (gt)
Nên EI là đường trung bình của ∆ ABC
⇒ EI // CD (tính chất đường trung bình của tam giác)
Và EI=CD/2
Trong tam giác ABC ta có:
I là trung điểm của AC
F là trung điểm của BC
Nên IF là đường trung bình của ∆ ABC
⇒ IF // AB (tính chất đường trung bình của tam giác)
Và IF=AB/2
b) Trong ∆ EIF ta có: EF ≤ EI + IF (dấu “=” xảy ra khi E, I, F thẳng hàng)
Mà EI=\(\dfrac{CD}{2}\); IF=\(\dfrac{AB}{2}\) (chứng minh trên) ⇒EF≤\(\dfrac{CD}{2}+\dfrac{AB}{2}\)
Vậy EF≤\(\dfrac{AB+CD}{2}\) (dấu bằng xảy ra khi AB // CD)
Tick nha 😘
a) Xét ΔACD có
I là trung điểm của AC
E là trung điểm của AD
Do đó: EI là đường trung bình của ΔACD
Suy ra: EI//CD
Xét ΔABC có
I là trung điểm của AC
F là trung điểm của BC
Do đó: IF là đường trung bình của ΔABC
Suy ra: IF//AB
Bài 27 (trang 80 SGK Toán 8 Tập 1): Cho tứ giác ABCD. Gọi E, F, K theo thứ tự là trung điểm của AD, BC, AC.
c) Khi EF =\(\dfrac{AB+CD}{2}\) thì tứ giác ABCD là hình gì.
HAHA![]()
![]() đố làm được ha
đố làm được ha
c: Ta có: \(EF\le KE+KF\)
\(\Leftrightarrow EF\le\dfrac{DC+AB}{2}\)
Dấu '='xảy ra khi E,K,F thẳng hàng
hay EF//AB//DC
Suy ra: ABCD là hình thang