Question

Cho tứ giác ABCD. Gọi E, F, I theo thứ tự là trung điểm của AD, BC, AC. 

Chứng minh rằng:

a)  EI//CD, IF//AB.

b)EF=<AB+CD/2

Answer 1

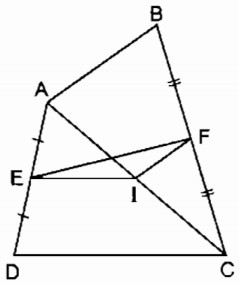
a) Trong tam giác ADC, ta có:

E là trung điểm của AD (gt)

I là trung điểm của AC (gt)

Nên EI là đường trung bình của ∆ ABC

⇒ EI // CD (tính chất đường trung bình của tam giác)

Và EI=CD/2

Trong tam giác ABC ta có:

I là trung điểm của AC

F là trung điểm của BC

Nên IF là đường trung bình của ∆ ABC

⇒ IF // AB (tính chất đường trung bình của tam giác)

Và IF=AB/2

 

b) Trong ∆ EIF ta có: EF ≤ EI + IF (dấu “=” xảy ra khi E, I, F thẳng hàng)

Mà EI=\(\dfrac{CD}{2}\); IF=\(\dfrac{AB}{2}\) (chứng minh trên) ⇒EF≤\(\dfrac{CD}{2}+\dfrac{AB}{2}\)

Vậy EF≤\(\dfrac{AB+CD}{2}\) (dấu bằng xảy ra khi AB // CD)

Tick nha 😘

Answer 2

a) Xét ΔACD có 

I là trung điểm của AC

E là trung điểm của AD

Do đó: EI là đường trung bình của ΔACD

Suy ra: EI//CD

Xét ΔABC có 

I là trung điểm của AC

F là trung điểm của BC

Do đó: IF là đường trung bình của ΔABC

Suy ra: IF//AB