Cho tam giác ABC ( AB < AC) có 3 góc nhọn nội tiếp (O). AH là đường cao của tam giác ABC. Kẻ đường kính AD của (O). Từ 2 điểm B,C kẻ BE và CF vuông góc với AD lần lượt tại E,F.
Gọi I là trung điểm của BC. Chứng minh IE = IF.

Những câu hỏi liên quan
Cho tam giác ABC (AB <AC) có 3 góc nhọn nội tiếp trong đường tròn (O; R). Vẽ đường
cao AH của tam giác ABC, đường kính AD của đường tròn. Gọi E, F lần lượt là chân đường vuông
góc kẻ từ C và B xuông đường thẳng AD. M là trung điểm của BC.
a) Chứng minh tứ giác BMOF nội tiếp.
b) Gọi K là giao điểm của AD và BC. Chứng minh KH.ED = KE.BH
a)
Xét (O) có
M là trung điểm của dây BC(gt)
nên OM\(\perp\)BC(Định lí đường kính vuông góc với dây)
Xét tứ giác BMOF có
\(\widehat{BFO}+\widehat{BMO}=180^0\left(90^0+90^0=180^0\right)\)
nên BMOF là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
Đúng 3
Bình luận (0)
Cho tam giác ABC (AB AC) có 3 góc nhọn nội tiếp trong đường tròn (O; R). Vẽ đường cao AH của tam giác ABC, đường kính AD của đường tròn. Gọi E, F lần lượt là chân đường vuông góc kẻ từ C và B xuống đường thẳng AD. M là trung điểm của BC.Tìm khẳng định sai ? A. Tứ giác ABHF nội tiếp B. Tứ giác BMFO nội tiếp. C.
H
E
/
/
B
D
D. Có ít nhất một khẳng định sai
Đọc tiếp
Cho tam giác ABC (AB < AC) có 3 góc nhọn nội tiếp trong đường tròn (O; R). Vẽ đường cao AH của tam giác ABC, đường kính AD của đường tròn. Gọi E, F lần lượt là chân đường vuông góc kẻ từ C và B xuống đường thẳng AD. M là trung điểm của BC.
Tìm khẳng định sai ?
A. Tứ giác ABHF nội tiếp
B. Tứ giác BMFO nội tiếp.
C. H E / / B D
D. Có ít nhất một khẳng định sai
Chọn đáp án D

* Chứng minh các tứ giác ABHF và BMFO nội tiếp.
- Từ giả thiết suy ra: 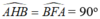
=> H và F thuộc đường tròn đường kính AB (quỹ tích cung chứa góc)
Vậy tứ giác ABHF nội tiếp đường tròn đường kính AB
- Gọi M là trung điểm của BC (gt), suy ra: OM ⊥ BC
Khi đó: 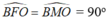
Nên M, F thuộc đường tròn đường kính OB(quỹ tích cung chứa góc).
Vậy tứ giác BMOF nội tiếp đường tròn đường kính OB
* Chứng minh HE // BD.
Dễ chứng minh tứ giác ACEH nội tiếp đường tròn đường kính AC.
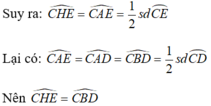
Và chúng ở vị trí so le trong suy ra: HE // BD
Đúng 0
Bình luận (0)
Cho tam giác ABC (AB<AC) nội tiếp đường tròn (O), kẻ đường cao AH của của tam giác ABC. Gọi M và N thứ tự là trung điểm của AB và BC, kẻ đường kính AD của đường tròn (O). Kẻ BE và CF vuông góc với AD tại E và F. CMR
1, Tứ giác ABEH nội tiếp.
2, MN vuông góc với HE
3, N là tâm đường tròn ngoại tiế tam giác HEF
Cho tam giác ABC nhọn (AB AC). Các đường cao AD, BM, CN của tam giác ABC cắt nhau tại H. Gọi O là trung điểm của BC, E là điểm đối xứng của H qua O. Kẻ CF vuông góc với BE tại F. Gọi K,L, R lần lượt là chân đường vuông góc kẻ từ N đến AC, AD, BC. Gọi giao điểm của DM và CN là S. CMR:1. Ba điểm K, L, R thẳng hàng2. HN.CS NC.SH3. Tia phân giác của góc BAC cắt BC tại I, kẻ đường thẳng đi qua C và vuông góc với đường thẳng AI tại P, đường thẳng CP cắt đường thẳng AO tại Q. Gọi G là trung điểm của...
Đọc tiếp
Cho tam giác ABC nhọn (AB < AC). Các đường cao AD, BM, CN của tam giác ABC cắt nhau tại H. Gọi O là trung điểm của BC, E là điểm đối xứng của H qua O. Kẻ CF vuông góc với BE tại F. Gọi K,L, R lần lượt là chân đường vuông góc kẻ từ N đến AC, AD, BC. Gọi giao điểm của DM và CN là S. CMR:
1. Ba điểm K, L, R thẳng hàng
2. HN.CS = NC.SH
3. Tia phân giác của góc BAC cắt BC tại I, kẻ đường thẳng đi qua C và vuông góc với đường thẳng AI tại P, đường thẳng CP cắt đường thẳng AO tại Q. Gọi G là trung điểm của đoạn thẳng IQ. CMR: đường thẳng PG đi qua trung điểm của đoạn thẳng AC
Cho tam giác ABC nhọn nội tiếp (O) đường kính AD, đường cao AH, Kẻ BE vuông góc với AD, kẻ CF vuông góc AD, (E,F thuộc AD), M là trung điểm của BC. Chứng minh M là tâm đường tròn ngoại tiếp tam giác HEF
Cho tam giác ABC có ba góc nhọn và AB < AC, nội tiếp (O; R) Vẽ đường kính AD của (O). Kẻ BE và CF vuông góc với AD (E, F thuộc AD). Kẻ AH vuông góc với BC (H thuộc BC)
1, Chứng minh: Bốn điểm A, B, H, E cùng thuộc một đường tròn
2, Gọi M là trung điểm của BC. Chứng minh: HE // CD và ME = MF
3, Gọi S là diện tích tam giác ABC. Chứng minh: 4S.R = AB.AC.BC
Cho tam giác ABC nhọn có AB<AC và nội tiếp đươngf tròn O đường kính AD. Gọi AH là đường cao của tam giác ABC. Qua B kẻ đường thẳng vuông góc với đường thẳng AD tại E.
a) cm: 2 HE vuong góc với AC
b) gọi F là hình chiếu vuông góc của điểm C lên đường thẳng AD và M là trung điểm của BC. Chứng minh M là tâm dường tròn ngoại tiếp tam giác HEF
Cho tam giác nhọn ABC (AB AC ) nội tiếp đường tròn (O). Kẻ đường cao AH của tam giác ABC và đường kính AD của đường tròn (O). Từ hai điểm B và C kẻ BE ⊥ AD tại E và CF ⊥ AD tại F. a. Chứng minh rằng tứ giác ABHE nội tiếp. b. Chứng minh rằng HE / /CD. c. Gọi I là trung điểm của BC. Chứng minh rằng IE IF .
Đọc tiếp
Cho tam giác nhọn ABC (AB < AC ) nội tiếp đường tròn (O). Kẻ đường cao AH của tam giác ABC và đường kính AD của đường tròn (O). Từ hai điểm B và C kẻ BE ⊥ AD tại E và CF ⊥ AD tại F.
a. Chứng minh rằng tứ giác ABHE nội tiếp.
b. Chứng minh rằng HE / /CD.
c. Gọi I là trung điểm của BC. Chứng minh rằng IE = IF .
a: góc AEB=góc AHB=90 độ
=>ABHE nội tiếp
b: góc HED=góc ABC=1/2*sđ cung AC=góc ADC
=>HE//CD
Đúng 1
Bình luận (0)
Câu 8(3 điểm): Cho tam giác ABC nhọn (AB AC) nội tiếp đường tròn (O; R). Vẽ đường cao AH của tam giác ABC và đường kính AD của (O). a) Chứng minh hệ thức: AB.AC AH. AD. b) Vẽ BE và CF lần lượt vuông góc với AD (E và F thuộc AD ). Chứng minh rằng HE vuông góc AC và HF vuông góc AB. c) Gọi M là trung điểm BC. Chứng minh rằng M là tâm đường tròn ngoại tiếp tam giác EHF.
Đọc tiếp
Câu 8(3 điểm): Cho tam giác ABC nhọn (AB < AC) nội tiếp đường tròn (O; R). Vẽ đường cao
AH của tam giác ABC và đường kính AD của (O).
a) Chứng minh hệ thức: AB.AC =AH. AD.
b) Vẽ BE và CF lần lượt vuông góc với AD (E và F thuộc AD ). Chứng minh rằng HE vuông góc AC và HF vuông góc AB.
c) Gọi M là trung điểm BC. Chứng minh rằng M là tâm đường tròn ngoại tiếp tam giác EHF.
a: Xet (O) có
ΔACD nội tiếp
AD là đường kính
=>ΔACD vuông tại C
Xét ΔACD vuông tại C và ΔAHB vuông tại H có
góc ADC=góc ABH
=>ΔACD đồng dạng với ΔAHB
=>AC/AH=AD/AB và góc CAD=góc HAB
=>AC*AB=AD*AH và góc CAH=góc BAD
b: Xét tứ giác ABHE có
góc AHB=góc AEB=90 độ
=>ABHE là tứ giác nội tiếp
=>góc AHE=góc ABE
=>góc AHE+góc HAC=90 độ
=>HE vuông góc AC
Xét tứ giác AHFC có
góc AHC=góc AFC=90 độ
=>AHFC là tứ giác nội tiếp
=>góc HFA=góc HCA
=>góc HFA+góc BAD=90 độ
=>HF vuông góc AB
Đúng 2
Bình luận (0)













