A là một điểm nằm trên đường tròn tâm O bán kính R. Đường thẳng AO cắt đường tròn tại điểm thứ hai là B. Đoạn thẳng AB được gọi là :
A; bán kính
B; đường kính
C; cung
D; cad B và C đều đúng mong mn giúp mình nhang lên nha cảm ơn
A là một điểm nằm trên đường tròn tâm O, bán kính R. Đường tròn Ao cắt đường tròn tại điểm thứ hai là B. Đoạn thẳng AB gọi là:
A. Bán kính
B. Đường kính
C. Cung
D. Cả B và C đều đúng.
cho đường tròn tâm o bán kính r và điểm a nằm ngoài đường tròn. đường tròn đường kính oa cắt đường tròn tâm o bán kính r tại m và n, đường thẳng đi qua a cắt đường tròn tâm o bán kính r tại b và c. b thuộc đoạn ac. gọi h là trung điểm của bc.
a) am là tiếp tuyến của đường tròn tâm o bán kính r.
b) Đường thẳng qua B vuông góc với OM cắt MN tại d. chứng minh
1) góc AHN = góc BDN
2) DH // MC
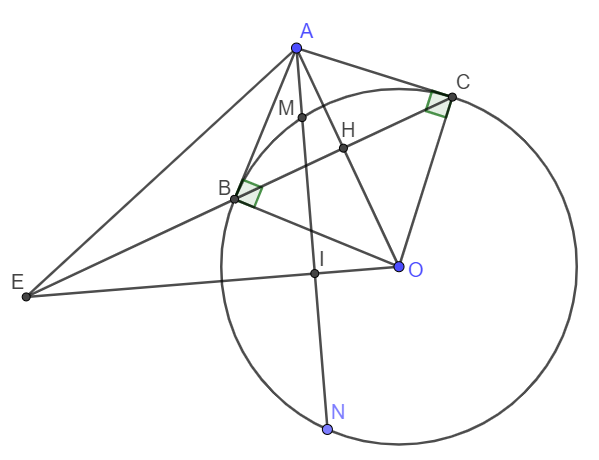
Cho đường tròn tâm $O$ bán kính $R$ và một điểm $A$ nằm ngoài đường tròn. Kẻ một đường thẳng đi qua $A$ và không đi qua $O$, cắt đường tròn tại hai điểm phân biệt $M$, $N$ ($M$ nằm giữa $A$ và $N$). Từ $A$ vẽ hai tiếp tuyến $AB$ và $AC$ với $(O)$ ($B$, $C$ là hai tiếp điểm). Đường thẳng $BC$ cắt $AO$ tại $H$. Gọi $I$ là trung điểm của $MN$. Đường thẳng $OI$ cắt đường thẳng $BC$ tại $E$. Chứng minh $AHIE$ là tứ giác nội tiếp.
Ta có
\(AB=AC\) (Hai tiếp tuyến cùng xp từ 1 điểm thì khoảng cách từ điểm đó đến hai tiếp điểm bằng nhau)
\(\Rightarrow\Delta ABC\) cân tại A (1)
AO là phân giác của \(\widehat{BAC}\) (Hai tiếp tuyến cùng xp từ 1 điểm thì đường nối điểm đó với tâm của đường tròn là phân iacs của góc tạo bởi 2 tiếp tuyến) (2)
Từ (1) và (2) \(\Rightarrow AH\perp BC\) (Trong tg cân đường phân giác của góc ở đỉnh tg cân đồng thời là đường cao, đường trung trực...)
\(\Rightarrow\widehat{AHE}=90^o\) (*)
Ta có
\(OM=ON\) (Bán kính (O)) \(\Rightarrow\Delta OMN\) cân tại O
Ta có \(IM=IN\) (Giả thiết) => ON là đường trung tuyến của tg OMN
\(\Rightarrow OE\perp AN\) (Trong tg cân đường trung tuyến xuất phát từ đỉnh tg cân đồng thời là đường cao, đường trung trực...)
\(\Rightarrow\widehat{AIE}=90^o\) (**)
Từ (*) và (**) => I và H cùng nhìn AE dưới hai góc bằng nhau và bằng 90 độ => I và H nằm trên đường tròn đường kính AE nên 4 điểm A;H;I;E cùng nằm trên 1 đường tròn
Cho đường tròn tâm bán kính và một điểm nằm ngoài đường tròn. Kẻ một đường thẳng đi qua và không đi qua , cắt đường tròn tại hai điểm phân biệt , ( nằm giữa và ). Từ vẽ hai tiếp tuyến và với (, là hai tiếp điểm). Đường thẳng cắt tại . Gọi là trung điểm của . Đường thẳng cắt đường thẳng tại . Chứng minh là tứ giác nội tiếp.
theo gt, ta co:
là trung điểm của
Cho đường tròn tâm O bán kính R điểm A nằm ngoài đường trong tâm O sao cho AO=2R. từ A vẽ 2 tiếp tuyến AB,AC với đường tròn (BC là các tiếp điểm) đoạn thẳng OA cắt đường tròn tâm O tại I đường thẳng qua O và vuông góc với OB cắt AC tại K.Chứng minh rằng: a, Tam giác OAK cân tại A b,KI là tiếp tuyến của đường tròn tâm O
a: góc KOA+góc BOA=90 độ
góc KAO+góc COA=90 độ
mà góc BOA=góc COA
nên góc KOA=góc KAO
=>ΔKAO cân tại K
b: Xét ΔOBA vuông tại B có sin BAO=OB/OA=1/2
nên góc BAO=30 độ
=>góc BOA=60 độ
Xét ΔOBI có OB=OI và góc BOI=60 độ
nên ΔOBI đều
=>OI=OB=1/2OA=R
=>I là trung điểm của OA
ΔKAO cân tại K
mà KI là trung tuyến
nên KI vuông góc với OI
=>KI là tiếp tuyến của (O)
Từ điểm P nằm ngoài đường tròn tâm O bán kính R, kẻ hai tiếp tuyến PA.PB tới đường tròn (A,B là các tiếp điểm ).Gọi H là chân đường vuông góc kẻ từ A tới đường kính BC ,đoạn thẳng PC cắt AH tại E.
a, Chứng minh bốn điểm P,A,O,B cùng nằm trên một đường tròn
b,Chứng minh OB.AH=CH.PB và E là trung điểm của AH
c,Giả sử PO=d. Tính AH theo R và d
Cho đường tròn tâm O, bán kính R có đường kính AB cố định. C là một điểm thay đổi trên đường tròn (C khác A và B). Gọi H là hình chiếu của C trên AB, I là trung điểm của AC. Đường thẳng OI cắt tiếp tuyến tại A của đường tròn (O;R) tại M, đường thẳng MB cắt đường thẳng CH tại K. Chứng minh IK song song với AB
Vẽ hình thôi ạ
Cho đường tròn tâm O bán kính R và một điểm A nằm ngòi đường tròn . qua a kẻ tiếp tuyến AB với đường tròn (B là tiếp điểm) . tia Ax nằm giữa A,B và AO cắt đường tròn (O;R) tại hai điểm C và D( C nằm giữa A và D) . gọi M là trung điểm của dây CD , kẻ BH vuông góc với AO tại H . a,Tính OH. OA theo R .b, Chứng minh bốn điểm A,B,M,O cùng thuộc một đường tròn . c,Gọi E là giao của OM với HB . Chứng minh ED là tiếp tuyến của đường tròn
a: OH*OA=OB^2=R^2
b: ΔOCD cân tại O
mà OM là trung tuyến
nên OM vuông góc với CD
Xét tứ giác OMBA có
góc OMA=góc OBA=90 độ
nên OMBA là tứ giác nội tiếp
c: Xét ΔOHE vuông tại H và ΔOMA vuông tại M có
góc MOA chung
Do đó: ΔOHE đồng dạng với ΔOMA
=>OH/OM=OE/OA
=>OM*OE=OH*OA=R^2=OC^2=OD^2
=>ΔODE vuông tại D
=>DE là tiếp tuyến của (O)
cho đường tròn(o) bán kính R=6cm và một điểm A cách O khoảng 10cm. Từ A vẽ tiếp tuyến AB(B là tiếp điểm) với đường tròn tâm O. lấy điểm C trên đường tròn tâm O, tia AC cắt đường tròn tâm O tại điểm thứ hai là D. gọi I là trung điểm của CD
a/ tính độ dài đoạn thẳng AB
b/ khi C di chuyển trên đường tròn(o) thì I di chuyển trên đường nào?
c/ cm rằng tích AC.AD khồng đổi khi c thay đổi trên (o)
1. Cho đường tròn (A;1cm) và (B;1cm). Điểm A nằm trên đường tròn tâm B. Gọi C là điểm nằm trên cả 2 đường tròn tâm A và tâm B. Giải thích tại sao AB=BC=CA.
2. Cho đoạn thẳng AB=4cm. Hãy nêu cách vẽ điểm M sao cho MA=3cm, MB=2cm.
3. Cho đoạn thẳng Ab=4cm. Gọi O là trung điểm của nó. Vẽ đường tròn (O;1cm) cắt đoạn OA tại M, cắt đoạn OB tại N.
a) Điểm M có là trung điểm của đoạn OA không?
b) Điểm N có là trung điểm của đoạn OB không?
c) Vẽ đường tròn có tâm trên đoạn thẳng AB có bán kính 2cm sao cho điểm M nằm bên trong đường trong, điểm N nằm bên ngoài đường tròn.
Cho đường tròn tâm O bán kính R và một điểm A nằm ngoài đường tròn . Qua A kẻ tiếp tuyến AB với đường tròn ( B là tiếp điểm ) . Vẽ tia Ax nằm giữa tia AB và tia AO cắt đường tròn (O) tại hai điểm C và D ( C nằm giữa A và D ) . Gọi M là trung điểm của dây CD , kẻ BH vuông góc với AO tại H .
a, Tính tích OH.OA theo R
b, chứng minh 4 điểm A , B , M , O cùng thuộc một đường tròn
c, Gọi E là giao điểm của OM với HB . Chứng minh ED là tiếp tuyến của đường tròn ( O;R )
a: OH*OA=OB^2=R^2
b: ΔOCD cân tại O
mà OM là trung tuyến
nên OM vuông góc với CD
Xét tứ giác OMBA có
góc OMA=góc OBA=90 độ
nên OMBA là tứ giác nội tiếp
c: Xét ΔOHE vuông tại H và ΔOMA vuông tại M có
góc MOA chung
Do đó: ΔOHE đồng dạng với ΔOMA
=>OH/OM=OE/OA
=>OM*OE=OH*OA=R^2=OC^2=OD^2
=>ΔODE vuông tại D
=>DE là tiếp tuyến của (O)